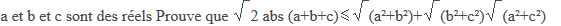Inferieur A

[baridomerre]

Salut tous le monde ;

Merci de voir la piece jointe
j'ai aucune idée meme le prof nous a donne cet enonce en explicant le groupe des nombre complex jarive pas a voire une relation entre les nombre Complex et l'enonce une clarifacation ou de la maniere sera tres utile merci
abs = valeur absolue et pour racine2 abs (a+b+c) = sqrt(2)*abs (a+b+c)
-----

[Gandhi33]

La pièce jointe n'est pas encore validée, peux-tu écrire le contenu dans un nouveau message ?

[baridomerre]

soit a et b et c trois réeels :
prouve que sqrt(2)*abs(a+b+s) ≤ sqrt(a²+b²) +sqrt (b²+c²) +sqrt (c²+a²)
abs = valeur absolue
Merci d'avance

[Gandhi33]

Super ! Je te conseilles d'utiliser l'inégalité quadratique et l'inégalité triangulaire.

[A voir en vidéo sur Futura]

[Gandhi33]

L'inégalité entre les moyennes quadratique et arithmétique dit que

L'inégalité triangulaire indique que

Cordialement

[baridomerre]

peut tu explique celle de L'inégalité entre les moyennes quadratique et arithmétique dit que parce quon a jamais etudier

[Gandhi33]

En fait je vais plutôt te montrer la démonstration utilisant les nombres complexes.

Tu peux inventer trois nombres complexes comme suit :

Si tu les additionnes membre à membre, tu obtiens d'où .


D'autre part, tu sais que .

Il ne reste plus qu'à montrer que ce qui est vrai par l'inégalité triangulaire.

Cordialement

NB: les inégalités sont disponibles ici http://webusers.imj-prg.fr/~razvan.b...equalities.pdf

[baridomerre]

Merci bcp Ghandi33

[Gandhi33]

Je t'en prie Vive la paix ! Vive gandhi ! Vive moi !