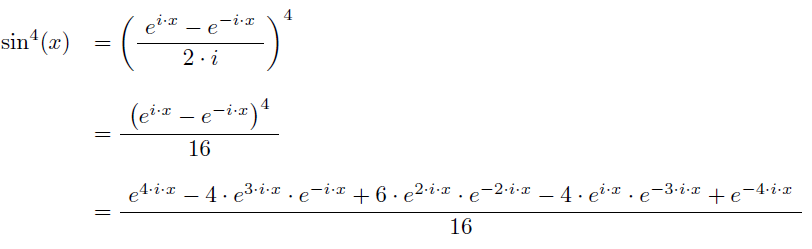intéret de la linearisation pour integrer fonctions trigo ???

[henry56]

Bonjour,

Je ne comprend pas tellement l'intérêt de linéariser sin^4x pour trouver sa primitive

méthode sans lineariser

primitive de u^n= (u^n+1)/ (n+1*u')
primitive de sin^4x = -(cos^5x)/(5*sinx)


si l'on souhaite l'intégrer sin^4x entre pi/4 et 0 par exemple cela fait -4*(2^1/2)/32*5*(2^1/2)/2 = -8*(2^1/2)/160*(2^1/2)= -1/20=-0.05


méthode en linéarisant


En linearisant je trouve sin^4x= 1/8cos4x-1/2cos2x+3/8 que j'intègre entre pi/4 et 0 ce qui donne 1/32sin(pi)-(1/4)sin2x+(3/8)pi - 0 = (3pi-8)/32 = -0.044


je trouve la première méthode beaucoup moins fastidieuse mais peut être que j'ai fait une erreur ??





ps: cos^4x = cos(x)^4
-----

[shezone]

bonjour henry56 ,

As-tu juste essayé de dériver ton expression de la primitive de sin(x)^4 ?

cdt

[henry56]

Peut etre que c'est parce que dans la premiere méthode je me retrouve avec un zéro en fraction -(cos (pi/4)^5)/ 5*sin (pi/4)- (-cos (0)^5)/ 5*sin (0))

[henry56]

Heu oui j'ai essayé

((-cos(x)^5)/(5*sinx))' = (5sin(x)


Heu oui en effet je suis

merci

[A voir en vidéo sur Futura]

[shezone]

Essaye de dériver ta primitive , et tu verras qu'elle sera fausse , c'est pour cela qu'on linéarise , car il n'y a pas de primitive évidente .

cdt

[shezone]

La dérivée que tu as mis est complètement fausse aussi , c'est un produit que tu as à dériver, donc il y a une formule que tu dois surement connaître vu que tu en es au cours sur les primitives

cdt

[henry56]

J'ai une autre question pourquoi dans cette exemple de linéarisation de mon cours le i (nombre imaginaire) au dénominateur disparaît à la deuxième fraction

[henry56]

Oui pour la dérivé j'ai pas finit mon calcul quand je me suis rendu compte que c'était une fonction de type u/v

[gg0]

" pourquoi dans cette exemple de linéarisation de mon cours le i (nombre imaginaire) au dénominateur disparaît " Fais le calcul, tu verras !!

Cordialement.

[shezone]

quel est le résultat de i² ?

cdt

[henry56]

Ok j'ai compris i²=-1 donc i^4=1

merci !