Pourquoi l'intégrale d'une fonction représente-t-elle l'aire sous la courbe ?

[rrricharddd]

Bonjour,

Je suis en TS, je n'ai pas vraiment de difficultés à faire mes exercices mais j'ai beaucoup de mal à comprendre pourquoi l'intégrale d'une fonction représente l'aire sous sa courbe représentative. Je comprends qu'il ait un lien, puisque l'aire sous la courbe , représentative de la fonction dépend directement de . (logique )
Et on sait que l'intégrale d'une fonction est aussi une des ses primitives car .

Donc l'aire sous la courbe dépend de et est la dérivée de la fonction , ainsi sur un intervalle quand est grand, l'aire sous la courbe augmente et le coefficient directeur () de la tangente des primitives (donc de l'intégrale) est grand donc, la valeur de l'intégrale augmente. Réciproquement quand l'aire ne varie pas, le coefficient directeur de la tangente des primitives est nul donc la valeur de l'intégrale est constante et enfin quand est négatif, l'aire diminue , le coefficient directeur de la tangente est négatif donc la valeur de l'intégrale diminue.
Je comprend donc qu'il y ait un lien mais je ne comprends pas pourquoi l'aire sous la courbe est égal à l'intégrale.

J'ai cherché de partout mais à chaque ils expliquent comment calculer l'aire sous la courbe mais pas pourquoi on agit de cette manière. N'y a-t-il pas une démonstration ou une analogie qui permettrait d'expliquer ou rendre plus compréhensible ce mécanisme ?

Je désir vraiment comprendre et maitriser parfaitement les outils que j'utilise quand je fais des mathématiques. Pour mieux comprendre les intégrales j'ai même lu un livre: En cheminant avec Kekeya mais celui-ci à part m'avoir apporté un contexte historique ne m'a rien apporté de plus que ce que je savais déjà (sur la dérivation et les intégrales).

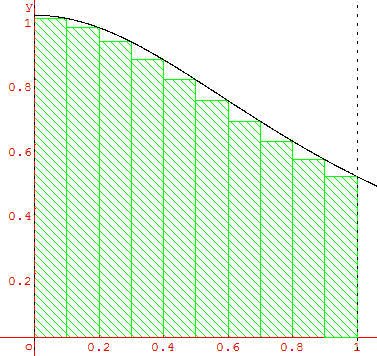
De plus on présente souvent l'aire sous la courbe d'une fonction comme la somme de rectangles d'une largeur qui tend vers 0.

En notant la largeur de ces rectangles on devrait avoir quelque chose du genre:

.
En appelant l'écart entre et on a:

.

Puis en dérivant par rapport à on devrait avoir:



Comme est la dérivée de l'intégrale on devrait avoir:

Mais j'ai du mal à continuer pour vérifier cette égalité.

Un peu d'éclaircissement serait très sympas

Merci d'avance
-----

[Tryss2]

Disons que le lien entre aire sous la courbe et intégrale est "évident", c'est le lien entre dérivée et intégrale qui l'est moins

En effet, l'intégrale, c'est, en gros, la limite de l'aire couverte par des rectangles sous la courbe quand leur largeur tend vers 0. On "voit" que la différence d'aire entre l'aire sous la courbe et celle des rectangles tend vers 0 quand les rectangles deviennent de plus en plus fin (enfin si la fonction est pas trop méchante).

Première question piège : comment définirai tu mathématiquement l'aire sous la courbe

Maintenant pour le lien entre dérivée et intégrale, celui ci est "expliqué" par un théorème :

Le théorème fondamental de l'analyse


Un problème dans ton idée de démonstration, c'est que ton dx dépend de t

[rrricharddd]

Merci d'avoir répondu

Je m'intéresserai au théorème fondamental de l'analyse.

Pour le je ne comprends pas pourquoi il dépend de , pour moi c'est juste un nombre très petit.

Sinon pour ma définition de l'aire sous la courbe de à je dirais: "Aire de la surface délimitée par la courbe et les droites d'équations , et ".
Après quand la courbe passe sous l'axe des abscisses je sais qu'il faut soustraire l'aire mais je ne sais pas si c'est dans mon programme, en tout cas je ne l'ai pas encore vu en cours

[gg0]

Bonjour.

peut-être une explication historique, en revenant à l'époque où on s'est aperçu que "le problème des aires et l'inverse de celui des tangentes" : Fermat, Leibnitz, Newton, entre autres, on commencé à mathématiser l'obtention de la tangente à une courbe, définissant ainsi la notion de dérivée. En appliquant cette idée à une surface située sous une courbe de fonction, on retrouva .. la fonction. Donc en inversant la procédure de dérivation, on va obtenir l'aire sous la courbe.
Ces notions sont restées longtemps assez intuitives (infiniment petits chez Leibnitz, par exemple) mais peuvent encore servir d'introduction à l'idée d'utiliser des primitives pour calculer les aires. Dans les présentations modernes, du niveau supérieur, on définit les aires par des techniques qui donnent des intégrales et on démontre le théorème fondamental de l'analyse qui fera le lien.

Tu peux reprendre ton schéma, et en supposant que l'aire sous la courbe est une fonction S(t) dérivables, voir que cette dérivée est la limite, quand dx tend vers 0 de (S(t)-S(t-dx))/dx.
S(t)-S(t-dx) est l'aire de la dernière tranche, sur ton dessin un peu plus grande que le rectangle vert, donc (S(t)-S(t-dx))/dx>f(t); de même, en considérant un rectangle de hauteur f(t-dx), on trouvera (S(t)-S(t-dx))/dx<f(t-dx)
On en déduit que la limite est comprise entre f(t-dx) et f(t) (suivant que la courbe descend ou monte), et comme dx tend vers 0, qu'elle est égale à f(t).

En fait, ce que j'ai fait est une petite tricherie, car une fonction continue peut parfaitement ne pas être décroissante, ni croissante, mais avec les propriétés des fonctions continues, on peut le justifier correctement.

Mais on a admis au départ que l'aire sous la courbe est bien définie et est une fonction dérivable ! C'est quand même une grosse supposition, et les matheux préfèrent définir l'aire d'une façon convenable (limite d'aires de rectangles, par exemple).

Enfin, dans ta preuve, il y a un gros problème : Tu es parti d'une égalité
.
qui n'est pas une égalité. Puis tu la dérives. Or deux fonctions presque égales peuvent avoir des dérivées très différentes, par exemple f(t)=2t et g(t)=2t+0,000000000sin(1000000 000000000t).
Elles ne diffèrent que de au plus un milliardième, mais leurs dérivées peuvent différer de un million !

Cordialement.

[A voir en vidéo sur Futura]

[Tryss2]

Pour le je ne comprends pas pourquoi il dépend de , pour moi c'est juste un nombre très petit.

Parce que dans ce que tu as écrit, t-a est un multiple de dx : il faut que la somme de la largeur des rectangles fasse la largeur de l'intervalle, sinon il y a un hic : donc quand tu bouges la taille de ton intervalle, tu va bouger la largeur des rectangles aussi

Sinon pour ma définition de l'aire sous la courbe de à je dirais: "Aire de la surface délimitée par la courbe et les droites d'équations , et ".

Oui, mais c'est quoi cette notion d'aire? Comment tu défini mathématiquement l'aire d'une surface?

Intuitivement, on voit bien ce que c'est, mathématiquement, beaucoup moins.

[rrricharddd]

Merci à vous deux je comprends beaucoup mieux

Donc si en gros si j'ai bien compris:

Quand tend vers





car tend vers

[gg0]

C'est plutôt f(t-dx); et il faut supposer f décroissante localement.

Avec toujours la question : C'est quoi, exactement, S(t) ?

[rrricharddd]

Oui effectivement j'ai pas fait attention en recopiant

[Cotissois31]

"pourquoi l'intégrale d'une fonction représente l'aire sous sa courbe représentative."

Comme dit précédemment, l'intégrale est par définition l'application qui fournit une valeur appelée "aire" pour tout domaine borné quelconque. L'aire n'aurait pas de définition suffisante sans l'intégrale.

Avec les carrés, on définissait l'aire comme la largeur au carré.
Avec les rectangles, on définissait l'aire comme la somme des carrés composant le rectangle.
Avec les polygones et les triangles, on ne pouvait plus définir l'aire sur la base de carrés. On définissait l'aire sur la base d'un rectangle qui subit des divisions. Un rectangle divisé en 2 est un triangle rectangle dont l'aire est moitié. D'où les innombrables formules d'aire, toutes dérivant de divisions astucieuses.
Avec les cercles, on approximait le résultat comme un polygone régulier à nombreux côtés, en se jurant qu'avec une infinité de côtés, on obtenait une valeur unique, normalisée par un nombre irrationnel pi. Toutes les opérations sur le cercle étaient donc normalisées par pi.

Pour tout domaine 2D borné :

1) soit on arrive à l'identifier comme une combinaison finie de polygones et de portions de cercle et on calcule l'aire comme la somme finie des aires, toutes étant connues par formule.

2) soit on écrit que l'aire est définie par un formalisme différentiel, l'intégrale. On dit que le domaine 2D bordé par une courbe f(x) et l'axe des x a une aire égale formellement à l'intégrale de f(x), en fonction des bornes évidemment. On écrit S f(x)dx, au sens où la valeur numérique de l'intégrale est égale à la somme d'une infinité de rectangles d'aire f(x)dx. Cette remarque est à la base de l'approximation numérique de l'intégrale, mais le mathématicien analyste écrira S f(x)dx sans y voir de somme explicite. Le calcul intégral est le domaine d'étude des transformations de l'intégrale, qui permettent d'obtenir des expressions très arrangeantes pour des problèmes particuliers.