Suite du type Un+1=f(un)

[YannickBOILOT]

Bonjour,

Je me permets de vous demander de l'aide sur un sujet

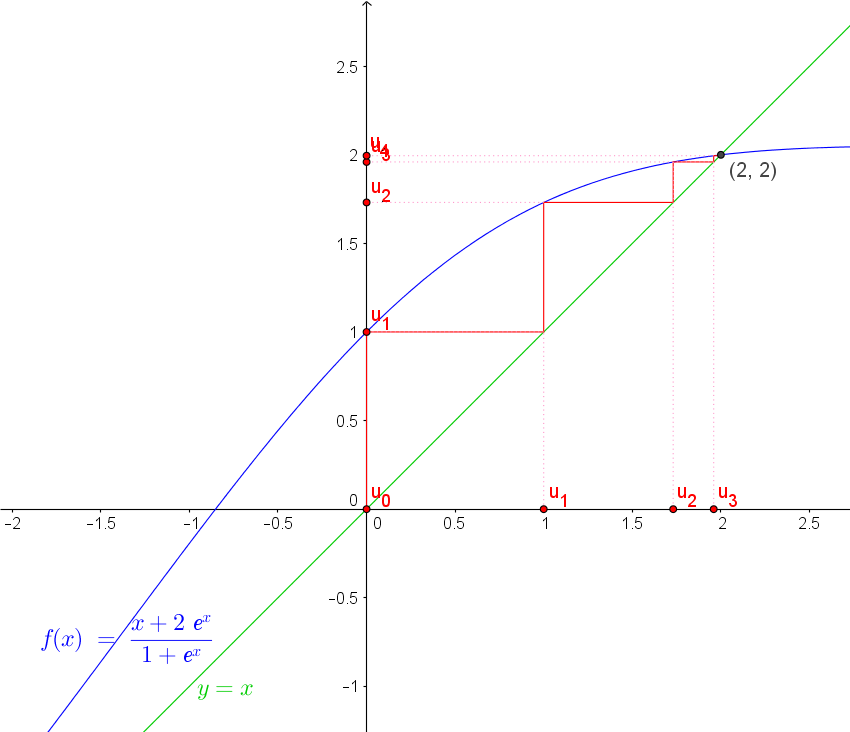
f(x)=(x+2exp(x))/(1+exp(x))

La suite u est définie par U0= 0 et pour tout nombre entier naturel n, Un+1= f(Un)

Démontrer que pour tout entier naturel n, 0 <2-Un+1 < 1/2(2-Un)
En déduire en raisonnant par récurrence que pour tout nombre entier naturel n, 0<2-Un<(1/2)^n+1

On pourra se servir des données suivantes : 2-f(x)= (2-x)*(1/1+exp(x)) et 0 inf Un inf Un+1 inf 2


A votre disposition si vous avez besoin de renseignements complémentaires, d'avance merci,
-----

[zenxbear]

ce genre d'exo repond toujours à la même démarche.

on fait un dessin, de cette suite, en partant de , qui ici vaut 0. ca donne ceci:

tu observes:

1- un point très particulier, de coordonnées (2,2), c'est un point fixe. intersection de la courge et . En gros, tu sais que 2 vérifie

2 - ta suite reste confinée entre 0 et 2.
La raison apparaît sur le dessin: f renvoie l'intervalle [0,2] sur l'intervalle . Donc une récurrence démontre ce résultat...
3 - ta suite est croissante. ie:
La raison apparaît aussi sur le dessin: la courbe représentant f est située au dessus de la droite y=x. En gros ... continue.

4 - ta suite semble converger vers le point fixe donc vers 2.

dans l'énoncé on te demande de ne pas te fatiguer à démontrer 2 et 3. Et on admet que
et de viser immédiatement le point 4. Et de regarder la suite .

et démontrer que :

ici: : est déjà vue, d'ailleurs si tu regardes bien, on te l'a mis sous les yeux dans l'énoncé.

pour qui est aussi ,
on te demande simplement d'utiliser la formule "2-f(x)= (2-x)*(1/1+exp(x)) "

[PlaneteF]

Bonsoir,

0<2-Un<(1/2)^n+1

Avec des parenthèses comme ceci : (1/2)^(n+1)

​Cordialement

[PlaneteF]

Bonjour,

2-f(x)= (2-x)*(1/1+exp(x))

Et là aussi des parenthèses manquantes, en fait tu viens d'écrire :

Rappel : https://fr.wikipedia.org/wiki/Ordre_des_op%C3%A9rations

Cdt

[A voir en vidéo sur Futura]

[YannickBOILOT]

Bonjour,
Merci a ZENXBEAR pour ses renseignements qui m'ont permis d'avancer
Pour Démontrer que pour tout entier naturel n, 0 <2-Un+1 < 1/2(2-Un), pas de souci, j'ai fait la démonstration
Par contre je bloque sur "En déduire en raisonnant par récurrence que pour tout nombre entier naturel n, 0<2-Un<(1/2)^(n+1)". L'initialisation ne me pose pas de soucis mais l'hérédité m'en pose un. Je n'arrive pas à retrouver une expression telle que 1/2(Vn).
Ensuite l'encadrement de 2-Un est OK, puisque lim (1/2)n= 0, donc 2-Un est encadré par 0, théorème des gendarmes et 2-Un tend vers 0, ce qui est logique car Un inf 2
Merci pour votre aide,

[zenxbear]

tu écris mal ta récurrence.

tu viens de démontrer pour tout m

ta propriété de récurrence au rang n est:

tu cherches une majoriation de ...