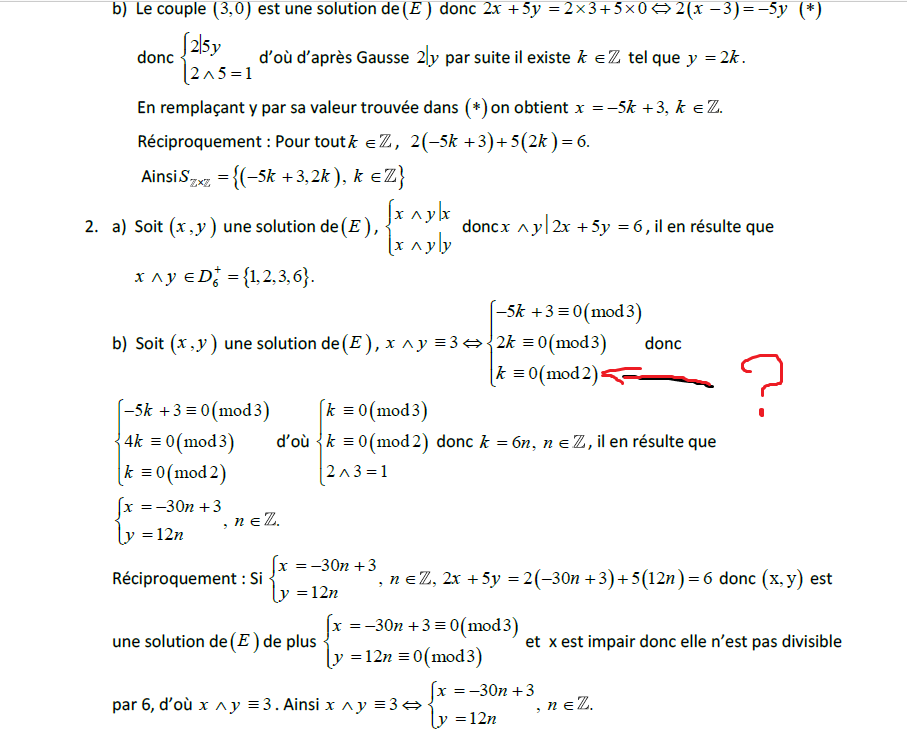Arithmetique

[skandertrifa]

Bonsoir ,

J'ai une question , voila l'exercice
(E): 2x+5y=6
1)Résoudre dans Z
réponse : Solutions dans Z^{2}={(-5k+3,2k) k € Z }
2) soit d=x^y , donnez les valeur possible
réponse: d|x , d|y donc d|2x+5y cad d|6 ou d€D6 {1,2,3,6}
3) determiner les couples (x,y) tel que x^y=3
voila la question que pose un probleme pour moi
ce que j'ai fait , j'ai sorti de x = 0 (mod3), mm chose pour y et j'ai conclus que k = 0(mod3) d'ou k=3n avec n apprtient a Z
Mais dans la correction il sort d'une systme
K =(mod2) , K = (mod3) => K = 0(mod6) , d'ou k=6n et il remplace ..
j'ai pas compris d'ou vient k = 0 (mod2) , j'ai besoin d'aider SVP
-----

[skandertrifa]

Voici la corrige de l'exercice , merci pour tt aide .

[ansset]

par contraposé :
si k congru à 1 (mod2) ( k=2p+1) alors
2k congru à 0 ( mod2) et
-5k+3=-5(2p+1)+3=-10p-2 congru à 0 (mod2)
d'où x^y congru à 2 et non 3.

[skandertrifa]

et comment je suis supposé de connaitre ca dans un devoir? ..

[A voir en vidéo sur Futura]

[ansset]

ma démo est en fait incomplète.

[ansset]

et comment je suis supposé de connaitre ca dans un devoir? ..

pas connaître mais déduire.
par contre je fini ,
on déduit que si k est impair 2 divise x^y ;
comme par hypothèse 3 divise x^y ; alors le pgcd de x^y serait 6 et non 3.
voilà, c'est plus clair.

[skandertrifa]

Ou on peut dire que dans multiples de 3, les nombres impaire sont seulement divisible par 3 et lesqui nbrs paires dont divisible par 6 et 3 donc un de x et y doit etre impaire comme y ne peut pas etre impaire donc x doit etre impaire d ou -5k+3 congru 0 mod2
D'ou vient k=0 (mod2)?
Et je veux savoir une petite regle generale quand j arrive a des cas comme ca par ex si on me fixe d=x^y=3 ou d appartient a Diviseurs de 9 comment je fais dans cas là et merci.

[ansset]

dans le 2a), on conclus que les plus grands diviseurs peuvent être {1,2,3,6}
dans le 2b) on suppose x^y=3 avec x=-5k+3 ; y=2k.
il est normal , comme on cherche les solutions de voir quelle peut être la parité de k dans ce cas.
Or, on montre que si k est impair, x et y sont divisible par 2 , or comme ils le sont par 3 (par l' hypothèse du cas cité), ils le sont par 6.
donc x^y=6 et non 3 , d'où k est pair et k congru à 0 (mod2)