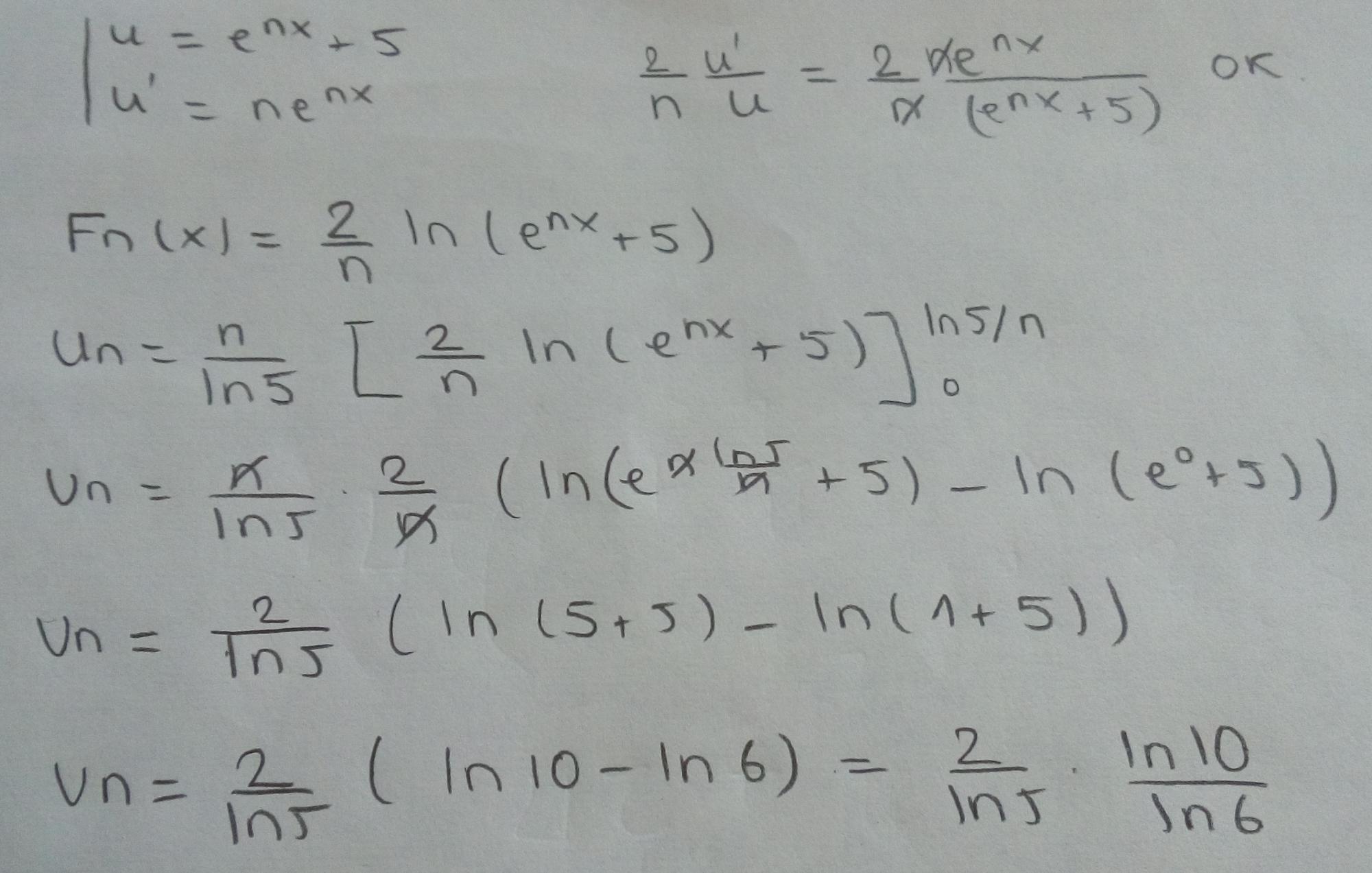Bonjour, j'ai un soucis sur une suite dont je dois montrer qu'elle est :
soit croissante ou décroissante ?
si elle est convergente ?
si elle est constante ?
Je vois que fn(x) et le quotient de termes positifs puisque 2e^nx > 0 et e^nx +5 > 0 mais je ne vois pas quoi faire en suite ....
Voila j'attends avec impatience votre aide
Bonjour
Un est calculable facilement, le numérateur de Fn(x) est presque égal à la dérivée du dénominateur, donc Fn est du type k*u'/u de primitive k*Ln(u), u étant une fonction à déterminer
Voici ce que je trouve , mais je ne suis pas sure de mon résultat .... dans ce cas la suite est constance et convergente ?
Bonsoir.
le calcul est correct jusqu'au début de la dernière ligne, seul le résultat final est faux.
Rappel : calculer, c'est appliquer strictement les règles, pas les imiter.
Cordialement.
Oups alors ça donne plutôt:
(2/ln5). ln(10/6)
donc la suite est constante et donc converge (toute suite constante est convergente non ? )
oui une suite constante est bien sur convergente
Merci de votre aide
Oups désolé j'ai encore un doute mais sur une autre suite, voici la question :
Alors selon moi Vn peut converger vers racine 2 / 2 pour Un = Pi/4 modulo 2 pi ou Un = 3pi/4 modulo 2pi -> Un=2npi/4 ou 6npi/4
De même elle peut converger vers 1 pour Un=pi modulo 2pi - > Un=2npi
Et Vn peut converger ou diverger, cela dépend de Un donc Vn ne diverge pas et ne converge pas toujours ?
Cela est il correcte ? j'ai donc les réponses A et B de vraies
Merci
Serais-tu capable de donner des contre-exemples pour C et D ?Envoyé par anso91
Oups désolé j'ai encore un doute mais sur une autre suite, voici la question :
Pièce jointe 343675
Et Vn peut converger ou diverger, cela dépend de Un donc Vn ne diverge pas et ne converge pas toujours ?
Cela est il correcte ? j'ai donc les réponses A et B de vraies
Merci
Attention, un doit être une suite non constante. Ta justification de A et B est à reprendre, mais on peut faire plus précis, sans se contenter d'affirmer (en rédigeant une vraie preuve).
Autre chose : " Un=pi modulo 2pi - > Un=2npi" est faux ! si Un=2n.pi, alors Un ne vaut pas pi modulo 2.pi, mais 0.
Cordialement.
effectivement 2npi est faux, mais du coup l'idée est elle bonne ? même si la démonstration n'est pas exacte pour la A et la B, comment vous y prendriez vous ?
Autrement , je n'arrive pas à trouver d'exemples dans lesquelles la Vn va être divergente ... elle serait donc toujours convergente ?
quelle est la nature de Vn si Un=n ?
Vn = sin Un et Un = n , je trouve que la suite converge vers -0,98..... à la caculette.... après comment expliquer que lim sin N en l'infini -0,98, je ne sais pas.
c'est faux, essayes des chiffres au hasard ( et grands par exemple ).
Effectivement j'étais en degrés et non en radians. Du coup Vn peut diverger ou converger c'est bien ça ? Est ce que c'est quelque chose a savoir que sin n diverge ou il y a une "démonstration" ?
oui Vn peut être convergente ou divergente.
( divergente signifie simplement qu'elle n'est pas convergente )
elle est convergente
-si Un est convergente vers L , ou si toute sous suite de Un converge vers L ou pi-L ( même sinus ).
ps : en général on "sait" que sin(n) ne converge pas , mais on peut aussi le démontrer.
Okay c'est noté. Et si on a cos Un , j'ai regardé c'est pareil; ça peut diverger ou converger . C'est bien ça ?
tout à fait !
Super, merci à tous de votre aide
correction :
ou L+2k.pi, ou pi-L+2k.pi avec k quelconque.
Ce n'est pas vraiment un théorème à connaître, c'est tellement une évidence si on place les différents entiers successifs sur le cercle trigo pour voir ce que donne sin(n) pour n=0, 1, 2, 3, 4, 5, 6, 7, ...
D'autre part si Un prend seulement 2 valeurs, alternativement, de sinus différents, par exemple 1, -1, 1, -1, ..., que fait Vn ?
Cordialement.
Dans ce cas, la suite est alternée donc elle diverge normalement ?
Trop imprécis, une suite alternée peut converger (alternée = chaque terme est du signe contraire à celui du terme précédent).
Je ne vois pas dans quel cas une suite alternée peut converger, par exemple la suite (-1)^n fait -1,1,-1,1.... elle ne converge donc pas... avez vous un exemple de suite alternée qui converge ?
salut gg0
il me semble que tu n'es pas clair là, car c'est Vn qui est sensé être un sinus de Un!
Cdt
Ah oui effectivement je comprends,
Si on a un suite alternée type (-1)^n , alors un prend les valeurs -1,1,-1,1 donc elle diverge,
Mais Vn converge puisque que ca donne Vn = sin (-1) puis sin (1) donc toujours égal à 0 donc converge vers 0 (enfin constante même°
C'est bien ça ?
comment ça sin(1)=0 ?
Ah zut, j'étais sur les cos.
Bref du coup j'ai sin(-1)=- 0,84 en rad et sin (1)=0,84
Donc pour Vn = sin(Un) et n=(-1)^n je vais obtenir des valeurs qui alternent donc Vn diverge ... je ne comprends plus où vous voulez en venir en fait ?
c'est à gg0 de te répondre, car je ne sais pas moi même.
(-1)^n/n par exemple, converge vers 0.
