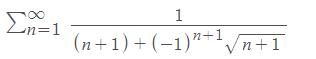Évaluer la convergence d'une série étrange

[invite1beccb6a]

Bonsoir ,

Je suis en ce moment en pleine préparation pour mon premier exam de Calcul différentiel et intégrale à l'université (mais comme c'est de la matière du collège , je post ici), et l'évaluation de la convergence d'une série particulière me cause problème , la voici :


En gros , je dois utiliser les critère de convergence pour déterminer si cette série converge vers une valeur ou non. (On cherche pas la valeur ici)



J'y vois une série alternée, mais comme elle oscille pas entre négatif et positif, je vois pas trop quelle critère utiliser...
J'ai essayer de décomposer par fraction partielle , mais j'ai pas l'impression que c'est une bonne piste..

Merci de votre aide !
-----

[gg0]

Bonjour.

Il ne s'agit pas en effet d'une série alternée, donc "J'y vois une série alternée" est une très mauvaise vue de la chose ! la présence dans le calcul d'un (-1)^n n'a rien à voir avec la définition d'une série alternée, revois la définition. En fait, c'est une série à termes positif et un simple critère de comparaison suffit.

Cordialement.

NB : "collège", sur ce site concerne les classes qu'on suit entre 10 et 15 ans. Donc pas de séries.

[jacknicklaus]

Une piste : décomposer selon une somme des n pairs + une somme des n impairs, et trouver deux minorants simples pour conclure.

[albanxiii]

Il y a plus simple, puisque tous les termes sont positifs.

[A voir en vidéo sur Futura]

[Amanuensis]

trouver deux minorants simples pour conclure.

Un seul suffit, non?

[invitedd63ac7a]

Effectivement !

[jacknicklaus]

Un seul suffit, non?

oui, en effet. inutile de compliquer !