Bonsoir,
Je suis élève de terminale S et cela fait désormais plus d'une heure et demie que je ne trouve pas la réponse à l'exercice suivant :
On définit la suite (Un) pour tout entier n >= 0 paret U(0) = 0
La suite (Vn) pour tout entier n >= 1 par Vn = n/(n+1)
Montrer par récurrence que pour tout entier n >= 1 , Un = Vn
Merci pour vos réponses.
-----



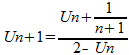 = (n+1)/(n+2).
= (n+1)/(n+2).