Problème avec une primitive

[Bert Zweisteine]

Bonjour à toutes et tous.

Je suis en train d'étudier les dérivées et primitives.

J'ai pris comme exemple les vitesse/accélération/distance parcourue pour faire un graphique.

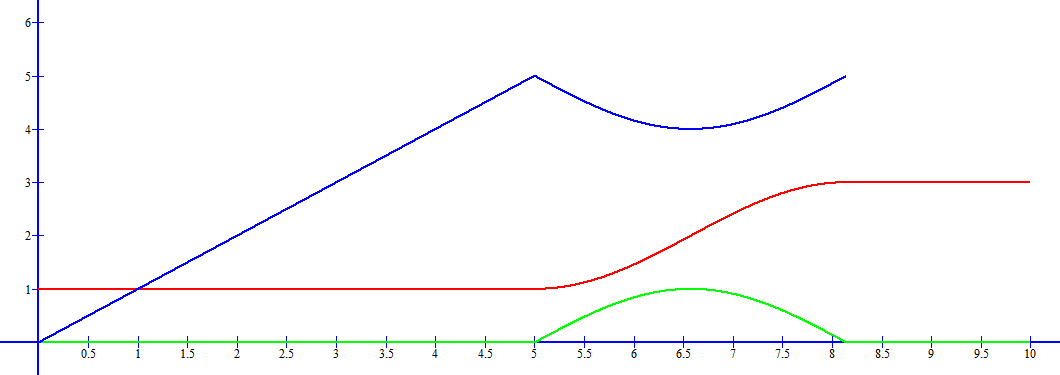
La vitesse est la fonction d'origine, en rouge.
L'accélération est la dérivée, en vert.
La distance parcourue est la primitive, en bleu.

Sur mon graphique, je commence par une vitesse de 1 (m/s)
L'accélération est de 0 (m/s/s) et la distance parcourue augmente régulièrement.

A partir du temps 5, j'ai voulu illustrer une augmentation de la vitesse en pente douce.
J'ai donc pris une courbe sinus de 270 à 450 degrés (ou de -90 à 90 degrés, c'est pareil)

Pour l'accélération, la dérivée du sinus étant le cosinus, la courbe me semble correcte.

Par contre, je bloque au niveau de la distance parcourue.

La primitive du sinus étant -cosinus, la courbe de distance parcourue redescend alors que la vitesse augmente.

Qu'est-ce que je fais de faux ?


-----

[gg0]

Heu ... entre 270° et 360°, le cos est négatif, donc -cos(x) >0. Et comme sin(270°)=-1, on fait mieux comme "pente douce".

Par contre, si tu travailles en degrés, la dérivée de sin n'est pas cos, et -cos n'est pas une primitive de sin.

Cordialement.

NB : Pour l'instant, je ne peux pas voir ton document ("en attente de validation").

[gg0]

Bon, maintenant je vois tes courbes, je ne sais pas ce que tu as fait, mais c'est n'importe quoi !! manifestement, tu ne tiens pas compte de la vitesse ( qui augmente de 1 jusqu'à 3). Par contre, tu as bien utilisé une vitesse négative (donc pas celle de la courbe en rouge) puisqu'on repart en arrière.

Sans tes calculs, on ne peut rien pour toi.

[Bert Zweisteine]

Heu ... entre 270° et 360°, le cos est négatif, donc -cos(x) >0. Et comme sin(270°)=-1, on fait mieux comme "pente douce".

Par contre, si tu travailles en degrés, la dérivée de sin n'est pas cos, et -cos n'est pas une primitive de sin.

Cordialement.

NB : Pour l'instant, je ne peux pas voir ton document ("en attente de validation").

C'est un peu pénible, ces attentes de validation...

A partir de 270 degrés, le cosinus part de zéro et augmente, non ?

De plus, je ne vois pas vraiment ce qui peut changer à la primitive si on parle en degrés ou en radians. Une fonction reste une fonction.

Ceci dit, je reste ouvert à toutes explications.

[A voir en vidéo sur Futura]

[Bert Zweisteine]

Bon, maintenant je vois tes courbes, je ne sais pas ce que tu as fait, mais c'est n'importe quoi !! manifestement, tu ne tiens pas compte de la vitesse ( qui augmente de 1 jusqu'à 3). Par contre, tu as bien utilisé une vitesse négative (donc pas celle de la courbe en rouge) puisqu'on repart en arrière.

Sans tes calculs, on ne peut rien pour toi.

De 0 jusqu'à 5, il me semble que mes courbes sont correctes.

Depuis 5, la vitesse augmente, la courbe de l'accélération me semble aussi correcte.

Je ne vois pas quels calculs je devrais fournir, il ne s'agit que de fonctions.

[gg0]

Heu ... je ne vois que des courbes (pas des fonctions, et aucune vraie explication sur le tracé de ces courbes :il n'y a pas de rapport évident entre 270° et 5 !!). Et je ne sais pas comment tu passes de l'une à l'autre (probablement là qu'il y a une erreur).

Je me suis effectivement un peu emmêlé les pinceaux entre sin et cos, vu que je ne travaille jamais en degrés (ce n'est pas l'outil des mathématiciens). Donc je rectifie :
de 270° à 360 °, le sinus varie de -1 à 0. Je ne vois aucun -1 pour 5, la vitesse est plutôt 1 et augmente doucement.

Donc comme tu n'as toujours pas dit ce que tu fais, impossible de savoir pourquoi c'est faux. Si la courbe de la vitesse est en rouge, la courbe de la position n'est pas celle en bleu. C'est tout.

[ID123]

il me semble que tu négliges un peu trop les constantes d'intégration. Si on part de l'accélération :
a = cos(t) pour une certaine plage de t à préciser.
==> vitesse = sin(t) + constante que tu vas régler pour que la vitesse se raccorde par continuité avec la vitesse initiale. Soit : v = v0 + sin(t).
==> position = v0.t - cos(t) + constante que tu vas régler pour que position se raccord avec ton choix de repère

tu verras alors que non, en aucun cas la position ne régresse alors que la vitesse reste toujours positive. Il faut être méticuleux sur le calcul des constantes d'intégration.

[Bert Zweisteine]

Merci pour vos réponses.

Alors je vais essayer d'être plus clair.

A la base, j'avais essayé de construire la relation Vitesse/Accélération/Position comme suit, mais, entre 5 et 8.14, j'ai voulu remplacer la droite sur l'image suivante par une courbe sinusoïdale pour être moins "brutal" dans le changement de vitesse.

2018-01-03 01_44_40-Graph.png

Finalement, les fonctions utilisées n'étaient pas tellement importantes, seule la cohérence dans les courbes importaient.

Mais effectivement, il y avait un problème de constante qui perturbait le résultat.

La courbe de vitesse, sinus de 270^o à 450^o a été "réhaussée" pour se mettre à la suite du 1, alors qu'en réalité, elle commence dans le négatif, donc en "marche arrière", ce qui explique la position qui régresse.

Donc, sur l'image suivante, on voit la courbe rouge en trait continu, qui est la fonction correcte pour calculer dérivée en vert et trait continu, ainsi que la primitive en bleu et trait continu qui est cette fois-ci correcte.

2018-01-03 03_00_16-Graph - C__Documents and Settings_Mandron_Desktop_Graph_Files_Vitesse-Acc-Po.png

Mais si je reprends ma volonté d'utiliser une fonction sinusoïdale pour la vitesse, j'ai tracé celle-ci en pointillé rouge.

L'accélération reste la courbe verte en trait continu car la constante +1 ne change rien.

Pour ce qui est de la distance parcourue (position), je retombe sur mon problème d'origine, à savoir que je ne sais pas comment la trouver.

Je suppose que ça doit ressembler à la courbe en pointillé bleu, c'est-à-dire la même forme que la vitesse.

Mais d'une part je n'en suis pas sûr, et d'autre part je ne sais pas comment la trouver.

Ce devrait être la dérivée de f(x)=sin(x+3/2*pi)+1.

Est-ce que mon raisonnement est correct ? (pour autant qu'il soit assez clair à comprendre)

Je précise que j'étudie tout seul et que je ne suis pas encore vraiment à l'aise avec toutes ces notions de dérivation et d'intégration.

[jacknicklaus]

il est difficile de te répondre sans un peu de maths. Je vois des graphes mais peu d'équations.

Il faut écrire explicitement les relations entre l'angle dont tu te sert comme paramètre (disons u), et les valeurs du temps t, de l'accélération, de la vitesse, de la position.Et ceci sur deux domaines de ton paramètre u : celui où l’accélération est nulle, puis celui où elle prend une forme en cos(u).

Ecris explicitement ce que tu connais :
- position x et vitesse v à t = 0
- relation entre u et t
- a = accélération à tout instant en fonction de u, et donc en fonction de t. Ecrire explicitement les équations dans chacun des deux domaines de validité : a = 0 de t = t0 à t1. Et a = f(t) de t= t1 à t = t2.


A partir ce celà, mais SEULEMENT à partir de çà, tu peux écrire les relations cinématiques : a = dv/dt et utiliser les conditions initiales. D'où v(t) sur les mêmes deux domaines [t0,t1] et [t1,t2]
Puis de même v = dx/dt et conditions initiales et de continuité sur x. d'où x(t) sur les deux domaines.

Et ENFIN tracer les graphes. J'ai l'impression que tu vas trop vite aux graphes sans avoir écrit soigneusement les maths qui vont bien.