Bonjour à tous,
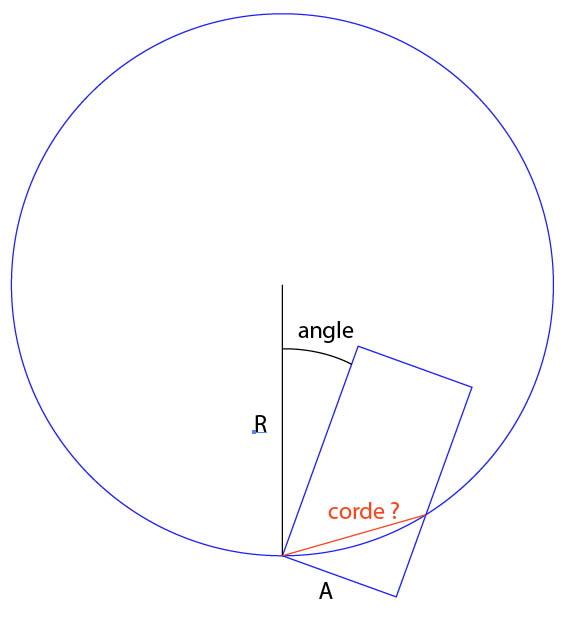
J'ai le rayon, l'angle et la longueur A, comment calculer la corde. Je planche dessus depuis un certain temps... Merci d'avance pour vos propositions
-----

Bonjour à tous,
J'ai le rayon, l'angle et la longueur A, comment calculer la corde. Je planche dessus depuis un certain temps... Merci d'avance pour vos propositions


info complémentaire, il est bien possible de calculer le point d'intersection entre le grand côté droit du rectangle et le cercle (la longueur de ce grand côté n'a pas d'importance, on suppose qu'il y a toujours intersection, il pourrait y avoir une deuxième intersection mais elle ne m'intéresse pas). Mais je recherche un moyen plus rapide, si existant, à partir des trois données initiales.

info complémentaire, il est bien possible de calculer le point d'intersection entre le grand côté droit du rectangle et le cercle (la longueur de ce grand côté n'a pas d'importance, on suppose qu'il y a toujours intersection, il pourrait y avoir une deuxième intersection mais elle ne m'intéresse pas). Mais je recherche un moyen plus rapide, si existant, à partir des trois données initiales.

Bonjour,
Connaissant la longueur C de la corde, on trouve facilement l'angle
Plus précisément, l'angle de la corde avec l'horizontale vaut arcsin(C/2R), et l'angle de la corde avec le coté A vaut arccos(A/C).
L'angle cherché vaut donc theta=-arcsin(C/2R)+arccos(A/C)
Mais il ne semble pas possible d'inverser cette équation pour trouver une formule explicite donnant C en fonction de theta. On ne peut la résoudre que numériquement.
Dernière modification par Resartus ; 10/04/2018 à 07h27.
Why, sometimes I've believed as many as six impossible things before breakfast

Bonjour Resartus,
et merci. J’ai recherché à partir de votre réflexion, je suis arrivé à cette équation :
A = COS(theta + arcsin(C/2R)) * C
(theta c’est bien mon angle qui est connu dans mon premier énoncé, prommis, la prochaine fois je nomme mes données)
Et là, je ne sais pas si l’on peut extraire la corde C ! c’est peut-être ce que vous dites en fin de réponse ?
Est-il possible de calculer X dans l’exemple suivant (de façon mathématique ou informatique) ?
arcsin(X) * X = 10
ou encore
sin(X) * X = 10

Bonjour.
En plaçant un repère orthonormé d'origine le bas du cercle, d'axe des y passant par le centre du cercle, on peut assez facilement déterminer l'équation du "petit côté" du rectangle (y=-x/tan(a), où a est la mesure de l'angle), puis les coordonnées du point M (le coin bas du rectangle), en utilisant OM=A (M(A/cos(a);-Asin(a)/cos²(a)) et enfin l'équation du côté passant par M. Enfin, on écrit que l'on cherche l'intersection de ce côté avec le cercle (équation x²+y²-2Rx=0), ce qui donne une équation du second degré ayant, si a et A conviennent deux solutions; reste à choisir la bonne. Puis calculer la longueur de la corde.
Les calculs sont faisables, mais assez abominables; je ne m'y risquerais pas (et les résultats que j'ai proposés sont aussi à vérifier).
Cordialement.


Bonjour,
Peut-être ainsi...(les calculs manuels sont dans l'appli)
Cordialement

Bonjour à vous et merci
A gg0 : oui comme je le dis plus haut, je peux calculer l'intersection grand côté du rectangle avec le cercle (merci wikipedia pour les formules), mais effectivement c'est lourd
A mécano41 : je n'ai pas d'application pouvant faire fonctionner l'appli jointe. J'ai juste pu ouvrir apparemment une copie d'écran, avec la note manuscrite et une partie données tableur, mais sans pouvoir saisir la moindre valeur. Dommage. Malgré cela, j'ai vérifié la longueur de corde sur une appli graphique (Adobe Illustrator), je trouve 54,389 et non 57,735 (pour les valeurs surlignées en jaune : 85 24 40). J'ai aussi essayé de suivre votre raisonnement, mais j'ai très vite abandonné, je ne sais même pas ce que c'est le signe E arrondi !


Bonjour,
Si tu n'as pas EXCEL, tu peux utiliser le logiciel gratuit Libre Office.
De toute manière, si tu peux lire les formules Sin et Cos, il te suffit de calculer les coeff. a, b et c que j'ai soulignés puis de les appliquer à la formule (ici, cas particulier, le dénominateur = 1)
Le E "arrondi c'est epsilon ; il y a plusieurs solutions en mettant une fois epsilon = 1 et une fois epsilon = -1 (attention au signe différent dans Sin et dans Cos)
Une fois que tu as le Sin et le Cos de l'angle, tu peux trouver celui-ci dans le bon quadrant...
Donne-nous tes trois valeurs, je les appliquerai pour vérifier...
Question : quelqu'un a-t-il vérifié mon calcul?
Cordialement

j'ai fait le test avec les valeurs que tu as saisies dans l'application, soit :
R = 85 mm
béta = 24
A = 40 mm
Tu obtiens une corde de 57,735 mm et en mesurant sur Illustrator la corde fait 54,389 (j'ai bien vérifié)
Sinon, j'ai téléchargé libre Office et je lis le fichier maintenant
J'ai intégré toutes les formules dans mon programme informatique (j'en n'ai pas parlé jusqu'à présent, mais ça importe peu), et j'obtiens les mêmes résultats qu'avec ton application, ce qui est logique.


Bonjour,
J'ai vérifié mes calculs et il y a une erreur dès la première ligne (sin au lieu de cos!).
Voici l'appli modifiée qui donne maintenant le bon résultat.
Pour information, j'ai ajouté la résolution détaillée d'une équation de la forme : a.cos + b.sin = c
Cordialement

bonjour,
Initialement, je m'attendais à une petite formule que tout le monde aurait pu trouver (sauf moi bien sûr !). Mais ça a été quand même plus costaud !
J'intègre ça ce soir et je te fais un retour, mais logiquement ça devrait marcher. D'ici là, merci déjà

Bonsoir,
Voilà c'est fait et ça marche bien sûr. Un grand merci donc mécano41, pour la démonstration et la solution. Je n'ai pas le niveau en math pour tout comprendre, mais j'ai quand même tenté.
Par curiosité, j'ai posé la question tout en haut, peut-on calculer x dans sin(X) * X = 10 ?


Bonjour,
Pour la question posée plus haut : "Est-il possible de calculer X dans l’exemple suivant (de façon mathématique ou informatique) ?
arcsin(X) * X = 10 ou encore sin(X) * X = 10 " :
Il faudrait reposer ta question dans un nouveau fil pour que d'autres intervenants la voient. Pour ma part je ne sais pas. J'ai fait une simulation graphique des deux cas, pour information.
Pour sin(X) * X = m, il y a une infinité de solutions (points d'intersection entre courbe bleue et courbe rouge). Evidemment, pour avoir une intersection, il faut augmenter x si m grandit. J'ai essayé d'en avoir au moins une à l'aide du solveur mais il semble perdre les pédales, même en mettant toutes les contraintes de limites...
Pour arcsin(X) * X = m, il y a deux solutions (deux points d'intersection entre courbe bleue et courbe rouge), x est un sinus donc limité à [-1 ; 1] et les limites pour m sont [0 ; pi/2].
Je n'ai pas essayé des résolutions par dichotomie car il faut du VBA et tu ne peux pas le lire.
Voilà à peu près tout ce que je peux te dire...
Cordialement

Bonjour,
Je ne vais pas poser la question dans un nouveau fil, je n'ai pas besoin d'approfondir là-dessus. J'ai posé la question pensant qu'il y avait peut-être une résolution simple. Je crois qu'il y a erreur de fichier joint !
Dichotomie, je ne connaissais pas ce terme. En fait c'est une méthode de calcul que j'ai utilisée plus d'une fois.
Merci mécano41 pour tout, continue d'être aussi passionné
Cordialement


Bonjour,
Erreur...bizarre!
Voici le bon.
Cordialement

merci pour le fichier. Etonnante la représentation graphique.
Cordialement

