Suite de nombres divisibles

[invite84127968]

Bonjour, sur mon tableur j'ai repéré les diviseurs avec un axe X incrémenté 1,1+1,1+1+1 etc bref 1,2,3,4,5.. et de la même manière pour l'axe Y.
Le résultat est une graphie qui ma parue familière, étant dans le monde agricole: en effet cela donne l'impression d'une plantation. sauf qu'au fond cela semble planté n'importe comment: n'importe quel paysan y verra tout de suite une "tournière", un semis dans une courbe.

ec.jpg
courbes.PNG

Donc je me suis intéressé à ces courbes en prenant comme nombre indiqué sur le graphe celui de l'axe des X, et j’obtiens des suites intéressantes, le centre de la courbe est pour les courbes partant d'un nombre impaires un carré: 81 pour 17. les carrés sont la somme des prédécesseurs impaires des nombres de départ: 17+15+13+11+9+7+6+5+3+1=81, pour le reste la formulation découle des tables de multiplication.
La courbe de départ 17 donne donc: [17,32,45,56,65,72,81,,72,65,56 ,45,32,17] avec comme construction: 17, (17+17-2), (17+17-2+17-4), (17+17-2+17-4+17-6).. , (17+1)/2 étant le nombre de fois où l'opération ce réitère jusqu'au carré le nombre d'élément de la courbe étant de 17, évidement on retrouve les diviseurs :[17/1,(17+17-2)/2, (17+17-2+17-4)/3, (17+17-2+17-4+17-6)/4....] > [17,16,15,14,13,12,11,10....1].

J’obtiens ce tableau:

17.jpg

Du coup je cherche à savoir si ces courbes sont étudiées et décrites, quelle sont les applications? les courbes indiquent que des nombres divisibles à l'exception de leur point de départ et d'arrivée. Il y a des doublons
De mon côté j'ai trouvé intéressant de les utiliser pour classer les nombres , trouver des règles dans leur agencement, regarder les intervalles etc..
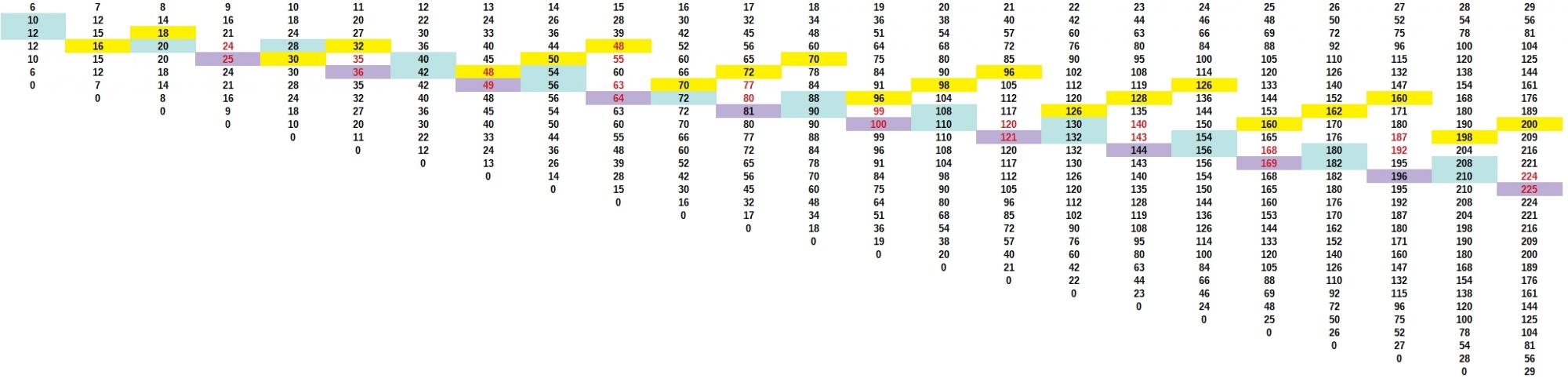
Ici j'ai regardé l'ordre d'apparition des nombres: la première apparition dans une courbe d'un semi premier est la dernière en donnant un code couleur (première apparition en rose),

clast.jpg
-----

[invite84127968]

J'ai décalé les courbes pour m’intéresser aux diagonales du tableau qui donnent les intervalles minimum entre deux nombres divisibles, si l'intervalle est de 2 alors un nombre premier se situe là .
j'obtiens de nouvelles suites:

ec22.jpg

et une nouvelle graphie de celle-ci:
esc.jpg


Bref pas mal de choses intéressantes et belles, l'objet de ce post est de savoir ou trouver de la littérature simple sur ces suites ?

[invite84127968]

Petite correction sur la localisation régulière de nombres premiers: ils sont en rouge (somme de deux nombres) dans une position régulière jusqu'à la courbe commençant par 29, cela ne veut pas dire que c'est une règle:

[invite84127968]

Ben me voilà classer dans la rubrique troll, semble-t-il.
J'envoie quand même un petit "up"
Mon but était de comprendre les séries et pouvoir écrire des fonctions.
Mon problème du moment est dans la formation des nombres, sachant qu'un nombre peut être défini comme la somme de ses prédécesseurs. Je suis donc parti sur l'idée qu'un nombre est le résultat d'une addition et j'ai pu établir une série d'additions pour chaque nombre. L'ensemble des additions d'un nombre étant calculable par prédécesseur, j'ai pu sur tableur établir une série qui m’intéresse au sens ou elle me semble fonctionner à la manière d'une horloge.En se penchant de près un nombre intègre bien des choses: par exemple le nombre de façons de former 14 par additions de 4 avec les prédécesseurs de 4 est égale à la somme des additions pouvant former 10 mais c'est aussi le dénombrement des sous ensembles des additions de 4 dans 14.
Dans ces séries les nombres divisibles finissent par rebond au nombre 0 pour les additions formées du même nombre.
Sans nom 1-1.jpg
J'ai pas mal de choses qui semblent intéressantes dans cette série dont l'une est de comprendre sa relation avec celle des produits citée dans mon autre post.
La série que je veux analyser est faite des sous ensembles de l'ensemble des additions formant un nombre par addition: dans onze il y a 11 additions de nombres différents avec 4, 10 avec 3....
Cela donne cela:
Sans nom 1-2.jpg
Bref si je ne parle pas tout seul voilà la façon de créer la série:
Capture.jpg
Désolé de ne pas avoir de capacités à formaliser tout cela mais le langage des formules n'est pas dans mes compétences malheureusement.

[A voir en vidéo sur Futura]

[eudea-panjclinne]

Si on considère la figure 17:
Axe des abscisses : x entier, axe des ordonnées descendant: y entier, la valeur en (x,y) est y(1+x)-y^2 pour x>y
Les courbes trouvées correspondent à la fonction y-->y(1+x)-y^2, x fixé
Pour les représenter dans le repère d'ici, on fait le changement de variable x->a :On a alors
y--->y(1+a)-y^2=x

On les représente dans le même repère par l'équation :
x=y(1+a)-y^2

C'est une famille de paraboles d'axe parallèles à (Ox) dans le repère d'ici.
Sauf erreur....

Vos dessins sont jolis, amusez-vous !
Leurs applications, essentiellement esthétiques.

[invite84127968]

Merci de ces infos et du compliment, ces paraboles sont donc banales dans le monde des nombres. Je les trouvent néanmoins intéressantes.

[invite84127968]

Bon, fin de semaine avec boulot chargé et état grippal..
Je donne donc quelques compléments pour ce qui concerne l’intérêt de ces séries à mes yeux.
J'ai constaté que chaque nombre dans chaque colonne ramené à son reste dans la division par le chiffre de la ligne dans laquelle il se situe par "rebonds" successifs:
-Par exemple, colonne L pour x=11 et y = 3 on a 10 (nombre d'additions ayant 3 comme plus grand terme pour formé 11), 10 est la somme de de 1+4+5 dans la colonne 8 (11-3), à noter que 1,4,5 sont les nombres de deuxièmes termes des additions, on rebondi ainsi pour finir sur une case vide: colonne C qui correspond à x=2 , on a bien 11/3= 3*3+2. Le nombre de rebonds est 3 (le diviseur). C'est une des propriétés.
Sans nom 1-1.jpg

Rmq:J'ai calculé pour y= 2 quelque soit x: le nombre d'additions dont le plus grand terme est 2 pour former x est pour les nombres paires: y=x/2 et impaires y=(x-1)/2 avec nombres de 2 dans l'ensemble de ces additions commençant par 2: (x^2+2x)/4 pour x paires et (2x|x+1|−x^2−2x−1)/8 . Je cherche maintenant à trouver la règle générale pour chaque y avec y variant de 1 à x.
Je cherche surtout à voir comment s’articule ces suites de fonctions et surtout à comprendre le rapport de ces dénombrements avec les suites de produits.
Pour mémoire colonne L du tableau des séries correspond à la colonne en rouge dans cette suite des additions pour former 11:
combi 2.jpg

[invite84127968]

Bon mon niveau de maths étant faible, pour ne pas dire nul j'avance doucement ( je me suis inscrit sur le MOOC de fun MOOC pour acquérir un socle de maths: j'ai du boulot).

Ne pas dire trop de conneries en postant ici n'est donc pas facile pour moi.

J'ai ré-envisagé la suite qui m’intéresse en tentant de définir ce qu'elle représente.
J'ai parlé jusqu'à présent d'ensemble des additions possible pour former un nombre.
Je me suis penché sur ce que cela pouvait être: combinaisons, arrangements , permutations etc.. et je n'ai pas trouvé de lien .
Je nommerai plutôt cela des "organisations" .
Un ensemble de 10 objets peut -être organisé de 42 façons différentes et les 42 façons comportent 275 sous ensembles.
Exemple: un chef de guerre veut défendre une position, il dispose d'un effectif de 10 guerriers, il peut placer ses soldats selon 42 organisations différentes:
de 10*1 guerriers pour dix positions occupées à 10 guerriers pour une position, en passant par l'ensemble des "organisations" possibles: 5,2,1,1,1 guerriers/ 5 positions / 7,3 guerriers/ 2 positions. J'ai décris le calcul du nombre "d'organisations".
La méthode calcul que j'ai trouvé pour le "nombre d'organisations" est peut-être une cousine de la suite de FIBONACCI dans la mesure ou il s'agit de faire la somme de sommes d'éléments de suites issues de prédécesseurs d'un nombre mais c'est plus compliqué à décrire, j'avais mis le schémas de construction sur tableur dans un post précédent: https://forums.futura-sciences.com/a...es-capture.jpg
L'analyse de l'établissement de l'ensemble "d'organisations" est riche d'informations aussi: on retrouve le nombre total des sous ensembles composant une organisation via la suite composant les premiers termes:
Pour le nombre 10:
Colonnes C,D,E,F,G :
adi 2.jpg
et le détail de ce qui est calculé au tableur:
adi.jpg

Je pense que cela doit être charabia ce que je décris ici, est-ce que quelqu'un comprends ce que je veux exprimer?

[ansset]

bjr,
je ne vois pas du tout où tu peux trouver un lien avec la suite de Fibonacci !!????
Cdt

[invite84127968]

En cherchant des suites faites de sommes pour comprendre celles qui m’intéresse je suis tombé sur la suite de Fibonacci, elle somme les 2 prédécesseurs d'un nombre: les suites que je décris sont faites aussi de sommes mais plus complexes dans la construction, plutôt que de dire des conneries j'ai préféré mettre cette construction sur tableur dans mon post n°4. Je te proposes de la construire pour me dire ce que tu en pense, si tu veux et que tu as confiance, je peux t'envoyer le fichier ODS.
Je cherche plus à comprendre ce qui se passe "en colonne" pour chaque nombre.
Tu as réussi à comprendre quelque chose dans mon discours? le fait que je ne possède pas de notions en maths est très handicapant pour moi.

[albanxiii]

Ben me voilà classer dans la rubrique troll, semble-t-il.

En fait, vous prenez ce forum pour un blog.

J'ai beau relire votre premier message, je ne comprends toujours pas de quoi vous parlez sur ce fil.

[invite84127968]

Je cherche juste des renseignements sur la relation de deux séries de suites, savoir si ces relations sont étudiées.
A la relecture du post je me rend compte que cela ne doit pas trop parler mon histoire.
Si vous en avez la patience,je tenterai demain de résumer plus clairement depuis le début la démarche.
Si à l'issue rien n'est plus claire alors je pense qu'il vaudra mieux en rester là .. charge à moi de revenir quand j'aurais le "langage" adapté si tant est que je puisse l'acquérir.

[ansset]

je pensais qu' eudea avait répondu assez justement sur la corrélation.
sa réponse ne te satisfait pas ?

[invite84127968]

Pour la suite Fig 17 oui, j'ai du coup utilisé cette construction. Pour la suite correspondant aux additions je n'ai pas trouvé de formule.

[invite84127968]

Bon je voulais faire une réponse simple et argumentée pour expliquer ma démarche peu claire et j'ai trouvé des réponses à force de chercher.
La suite qui m’intéresse est bien étudiée et décrite quelque part et elle est construite exactement sur le même schémas que le mien.
Il s'agit des partitions d'un entier. Je voulais raccrocher cette suite "partition" (et donc non pas organisation comme j'ai écrit dans un post précédent) à celle des sommes des prédécesseurs impaires: 17 donne 81 au centre de cette suite qui est (17,32,45,56,65,72,77,80,81,80 ,77,72,65,56,45,32,17). J'avais remarqué des éléments communs et c'est cela qui m’intéressait dans cette suite de prédécesseurs: trouver une accroche pour formuler celles des partitions.
Bref le travail est déjà à priori fait https://fr.wikipedia.org/wiki/Partit...e_construction , c'est bien trop complexe pour moi de retrouver ce que j'ai vu mais il semble que des formules soient déjà développées pour répondre à ma question initiale.
Ma question initiale d'ailleurs pas très compréhensible et pour laquelle il manque les trois quarts des infos: à ma décharge je traine un état grippale depuis un mois qui ne me laisse pas beaucoup d’énergie.

Donc voilà cela a du paraître un poil mystique mes histoires, je trouve cette approche par partition des nombre hyper intéressante, j'y trouve des analogies (sans rentrer dans un discours platonicien) avec les sciences de la nature, la croissance des plantes en particulier en regardant la structure des schémas de partition.
J'ai développé pas mal d'idées par analogie à ce sujet, en particulier celle d'une densité de ces structures et de zones de développements, mon langage n'étant pas mathématique je serais intéressé par une approche analogique de ces notions si quelqu'un en a connaissance je suis preneur (juste par curiosité).

Dans ma démarche j'ai développé les formules suivantes:

Pour la suite parabolique déjà écrite par Eudea: x*y-x^2+x plutôt que y(1+x)-y^2

Pour les partitions j'ai cherché pour l'ensemble commençant par le terme 2:

Nombre de partitions (avec 2 en 1er terme)= (x-1)/2
Pour les nombre impaires:
Nombre de 1= (x^2+2*x+1)/4
Nombre de 2=(2*x*abs(x+1)-x^2-2*x-1)/8

Pour les paires
Nombre de 1= (x^2+2*x)/4
Nombre de 2= (x^2+2*x+1)/8


Donc voilà quelques explications en souhaitant avoir apporté un peu de clarté à mon discours..

[invite84127968]

Bon je n'ai pas apporté de clarté semble t-il, un admin peut donc clore ce fil mort.. merci.