Calcul de coordonnées

**CharlyPoppins** · 06/03/2019, 14h52

Bonjour,

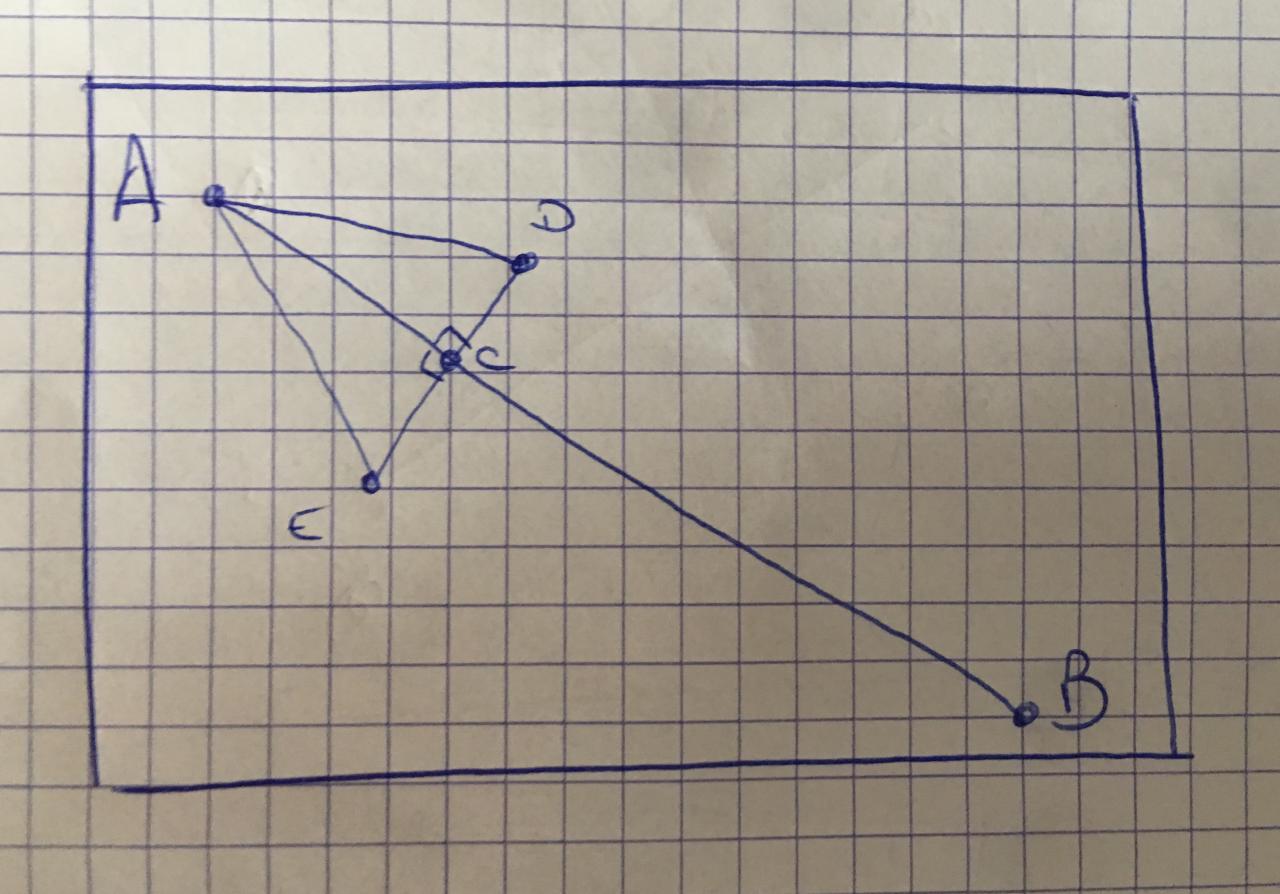
j'essaie de calculer les coordonnées des points D et E sachant A et B ainsi que la distance AC. (voir croquis).

L'idée est de construire une flèche en SVG

dynamiquement en fonction des coordonnées des points A et B.

Est-ce que vous avez des pistes ?

Nom : IMG_3863.jpg
Affichages : 105
Taille : 110,3 Ko

**albanxiii** · 06/03/2019, 18h45

Bonjour et bienvenue sur le forum,

Les coordonnées des points A et B ne sont pas suffisantes. Il faudrait par exemple la longueur AC (soit une valeur fixe, soit en pourcentage de la longueur AB selon la forme que vous désirez obtenir pour la flèche) et la longueur CD. Ou bien AC et l'angle au sommet de la flèche.

ps : il y a deux points C sur voter figure, je ne parle que de celui qui est sur la droite (AB).

**CharlyPoppins** · 07/03/2019, 08h09

Bonjour,

je reformule mon explication, je connais :
- les coordonnées du point A
- les coordonnées du point B
- la distance AC (pour l'exemple on peut considérer que AC = AB/5 )

Bien vu, je n'avais pas pensé à utiliser l'angle CAD.

Donc oui on considère que je connais également, soit l'u ou l'autre :
- soit l'angle CAD
- soit la distance CD

ps : Où est le deuxième point C ?

**gg0** · 07/03/2019, 08h52

Bonjour.

Dans les deux cas, on commence par placer C, à la distance AC de A en direction de B; donc
$\text{[math]}$
(traduction immédiate en termes de coordonnées (x,y) de C)

Avec la distance d = CD, on sait que D et E sont les intersections de la perpendiculaire en C à (AB) avec le cercle de centre C de rayon d. Ce qui donne un système de deux équations qu'on sait résoudre.
C'est un peu plus compliqué avec l'angle, mais on peut se ramener au cas précédent avec de la trigonométrie élémentaire.

Ce genre de question a été étudiée il y a plus de 50 ans par Donald Knuth, les détails sont sans doute dans son classique "the art of computer programming". Et il a étudié diverses façons de faire des flèches "bien équilibrées". Dans ton cas, le tracé de {AB], puis l'adaptation d'une flèche toute prête par translation (pointe en A), rotation (axe suivant AB) et homothétie (taille de la flèche) sera sans doute plus rapide et efficace pour avoir tous les cas (flèche longue ou courte, pointe plus ou moins effilée, etc.)

Cordialement.

A voir en vidéo sur Futura · Aujourd'hui

**CharlyPoppins** · 07/03/2019, 11h11

Ce qui donne un système de deux équations qu'on sait résoudre.

Qu'elles sont ces équations ? Et elles vont me permettre de trouver les coordonnées de D et E c'est bien ça ?

**gg0** · 07/03/2019, 11h59

(x-a)²+(y-b)²=r² où r est la rayon et a et b les coordonnées du centre
u(x-c)+v(y-d) = 0 où u et v sont les composantes du vecteur AC ( ou du vecteur AB) et c et d les coordonnées de C

C'est de la géométrie analytique élémentaire (niveau lycée).

**CharlyPoppins** · 07/03/2019, 15h40

Merci je vais essayer d'appliquer ces équations

C'est de la géométrie analytique élémentaire (niveau lycée).

Que j'ai oublié depuis bien longtemps ! Quand on ne pratique pas c'est compliqué...

**CharlyPoppins** · 11/03/2019, 10h25

Bonjour,

donc si j'ai bien compris (x-a)²+(y-b)²=r² est l'équation du cercle, du coup elle n'a pas de solution elle permet de vérifier qu'un point x,y appartient au cercle.

Par contre je ne comprend pas la deuxième ligne : u(x-c)+v(y-d) = 0 où u et v sont les composantes du vecteur AC ( ou du vecteur AB) et c et d les coordonnées de C

Est-ce que je n'ai pas plutôt de du vecteur CD ?

**gg0** · 11/03/2019, 10h30

Non, non, c'est bien ce que je disais. N'importe comment tu ne connais pas encore le vecteur CD.
La deuxième ligne est l'équation de la droite (CD) obtenue sans connaître D.

**CharlyPoppins** · 11/03/2019, 10h43

Du coup l'équation serait : (x-a)²+(y-b)²-r²=(x-a)+(y-b) avec a et b coordonnées du point C ?

**ansset** · 11/03/2019, 11h00

as tu une autre donnée, par exemple l'angle en A ?

**CharlyPoppins** · 11/03/2019, 11h14

Alors je ne sais pas quelle est la meilleure façon de calculer, mais dans mes paramètre soit je définirai l'angle CAD soit je définirai la longueur CD.

Donc pour un cas concret on peut considérer que l'on utilise un angle CAD de 15°.

**ansset** · 11/03/2019, 11h38

supposons donc $\text{[math]}$ ton angle CAD.
la trigo te donne AC/AD=cos( $\text{[math]}$ ) ( en distances )
soit AD=AC/cos( $\text{[math]}$ )
par pythagore, tu as
AD²=AC²+CD²
tu en déduis la longueur CD
et CD est perp à AB...
soit :
$\text{[math]}$ ( produit scalaire )....
à toi la suite.

**ansset** · 11/03/2019, 12h09

désolé : en plus direct.
$\text{[math]}$

**CharlyPoppins** · 11/03/2019, 13h54

Je suis d'accord avec tout ça, mais je ne comprend pas comment ça me donne les coordonnées du point D...

**ansset** · 11/03/2019, 14h44

pour trouver des coord il faut fixer une origine et des axes
supposons:
A(0,0)
B(14,-9) ( selon ton schéma) (*)
|AB| tu sais faire.( ou bien tu l'as déjà )
connaissant |AC| , tu en déduis immédiatement les coords de C(xc,yc) ( ou bien tu les as déjà )
soit D(xd,yd)
donc $\text{[math]}$

$\text{[math]}$ ( ou avec {AC} c'est idem )
ce qui te donne une première équation en xc,yc.
soit yc en fct de xc.( relation affine )
et
$\text{[math]}$
qui te donne une seconde équation.

le tout te donnera une equation du second degré en xc ( normal car les deux solutions correspondent aux deux points C et E)

(*) à remplacer par les bonnes valeurs si ton schéma n'est qu'illustratif.

ps: la solution par les cercles amène aussi à une équation du second degré.
elle est peut être plus rapide. ?

**CharlyPoppins** · 11/03/2019, 15h31

$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

Admettons que la longueur de la flèche soit 3

$\text{[math]}$
$\text{[math]}$

$\text{[math]}$ et $\text{[math]}$

c'est la que je bloque je ne trouve pas la correspondance avec l'équation linéraire, je cherche dans les cours en ligne.

Ensuite j'ai deux choix : calcul avec l'angle $\text{[math]}$ ou bien calcul de l'intersection du cercle de rayon $\text{[math]}$ et de centre $\text{[math]}$ avec la droite $\text{[math]}$ (passant par $\text{[math]}$ ) perpendiculaire à $\text{[math]}$ .

**gg0** · 11/03/2019, 16h00

Bonjour.

Le calcul de la longueur AB est manifestement faux, il y a déjà un écart horizontal de 14, et $\text{[math]}$ fait moins de 10. La bonne valeur est
$\text{[math]}$

Si la longueur de la flèche est AC=3 (*), alors les coordonnées x_C et y_C de C sont données par le calcul suivant
$\text{[math]}$
$\text{[math]}$

Tu en déduis la longueur CD, puis la valeur de $\text{[math]}$ et enfin l'équation du cercle.

Pour l'équation de droite, le calcul avec le produit scalaire donne exactement ce que j'ai suggéré au message #6, avec pour u et v les coordonnées du vecteur AB (Donc inutile de faire ce calcul, puisqu'une propriété classique, autrefois vue en première S et STI, permet d'écrire directement l'équation). L'équation est donc
$\text{[math]}$

Cordialement.

(*) pour une longueur de $\text{[math]}$ ça aurait fait une grosse flèche, plus de 30% du total ! Avec une flèche d'environ 16,6 de long c'est plus raisonnable.

**ansset** · 11/03/2019, 16h09

edit : grillé

**CharlyPoppins** · 11/03/2019, 16h45

Bien vu pour l'erreur de calcul de [TEX]AB[\TEX] j'ai du faire une fausse manip sur la calculatrice.

Je viens de comprendre ce que sont les composantes de vecteurs...

$\text{[math]}$ * $\text{[math]}$ = $\text{[math]}$

Si les vecteurs sont perpendiculaires avec le produit scalaire est égale à 0.

$\text{[math]}$ * $\text{[math]}$

$\text{[math]}$ = 0 est-ce juste ?

comment arrive-ton à $\text{[math]}$ ?

**ansset** · 11/03/2019, 16h59

Envoyé par CharlyPoppins

comment arrive-ton à $\text{[math]}$ ?

où as tu vu cela ?

**gg0** · 11/03/2019, 17h01

On n'y arrive pas.

Tu remplaces les valeurs connues, c'est tout. Tu verras bien ce que ça donne.

**ansset** · 11/03/2019, 17h06

Envoyé par CharlyPoppins

$\text{[math]}$ = 0 est-ce juste ?

Oui c'est juste, mais ça donne:
14(xD-xC)-9(yD-yC)=0
soit après simplification:
yD=(14/9)xD-((14/9)xC-yC)

edit : j'aurai du laisser calculer ....

**CharlyPoppins** · 12/03/2019, 10h12

Bonjour,

merci je comprend le cheminement jusque là.

Malheureusement @gg0 je ne peux pas remplacer par les valeurs connues car elles vont être dynamiques. Je dois donc construire un algorithme qui va me retourner deux solutions en fonction des valeurs passées en paramètre.

Je recapitule :

Les valeurs que je connais (plutôt connaitrais) (paramètres) $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ et $\text{[math]}$ .

Les valeurs que je dois trouver $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ et $\text{[math]}$ les coordonnées des deux points qui correspondent à l'équation (que je n'ai pas encore trouvée).

Je connais l'équation du cercle de centre $\text{[math]}$ et de rayon $\text{[math]}$ :

$\text{[math]}$

Je sais que $\text{[math]}$ et $\text{[math]}$ sont perpendiculaires donc $\text{[math]}$ avec $\text{[math]}$ et $\text{[math]}$ qui vont me permettre de trouver $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ et $\text{[math]}$ .

Donc j'ai l'équation :

$\text{[math]}$

$\text{[math]}$

De ce que j'ai trouvé je peux utiliser une équation paramétrique, mais je ne sais pas encore comment ça fonctionne

**ansset** · 12/03/2019, 10h22

bjr, il me semblait ( post #1 ) que tu connaissais les coords de A et B, ainsi que la distance AC, donc les coord de C.
tu peux donc simplifier tes équations.

**CharlyPoppins** · 12/03/2019, 10h29

Je le connais à un instant donné mais ça n'est pas être des valeurs fixes dans mon algorithme, elles doivent être paramétrables.

**gg0** · 12/03/2019, 10h35

J'ai utilisé ton exemple de valeurs pour les coordonnées de A et B, et la taille de la flèche, pour te faire comprendre les calculs. Puisque tu veux programmer, le minimum est que tu saches faire les calculs
* d'abord dans un cas parfaitement connu
* ensuite dans le cas général (avec des variables pour les coordonnées des points de base A et B et la taille de la flèche)
pour enfin transformer ça en un algorithme que tu comprends et que tu pourras coder.

Pour l'instant, tu ne montres pas ta capacité à faire la première étape (géométrie analytique élémentaire). Pour ma part, je me refuse à donner des formules toutes faites qu'un "informaticien" de type bidouilleur utilisera sans comprendre, renvoyant au formules qu'on lui a données les errances du programme. Si d'autres te les donnent, tant pis pour toi !

Et si tu veux vraiment finir par y arriver, commence par traiter vraiment le cas particulier que tu as proposé. Ça te fera une base de compréhension. Car il restera encore pas mal de soucis (ne serait-ce que la taille de la pointe, bien évidemment dépendante de la taille totale de la flèche).

Cordialement.

NB : Je ne sais pas avec quel langage tu codes, mais dans certains, il existe des librairie qui contiennent ce genre de tracé, déjà tout codé.

**ansset** · 12/03/2019, 10h53

remarque de forme :
sachant que c'est un algorithme sur des "proportions" et pas un exercice posé avec des valeurs fixes.
pourquoi avoir fait cette représentation en biais de ta flèche.
l'angle de celle ci est il un paramètre demandé, ou à prendre en compte ?
sinon, beaucoup plus simple de poser
A(0,0)
B(1,0) sur l'axe des abscisses de longueur 1 ( car tout le reste est prop à |AB| )
C(x,0) avec x<1
et ensuite choisir comme dernier paramètre soit r=|CD||CE| ou le demi-angle de la pointe.
les coords de D et E viennent tout de suite.

**CharlyPoppins** · 12/03/2019, 11h32

Avec d'autres valeurs pour que ce soit plus lisibles :
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

$\text{[math]}$
$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Jusque là est-ce que tout est bon ?

Comme dit en #1, le cas concret et de créer dynamiquement un polygone en SVG (c'est pour application react-native, le code utilisé pour les calculs est du Javascript et j'utilise une librairie pour afficher le SVG qui ne permet pas d'utiliser les Markers).

**gg0** · 12/03/2019, 11h39

Qu'as-tu fabriqué ??

Il y a l'équation d'un cercle et celle d'une droite, et on cherche les intersections, c'est à dire les valeurs de x et y qui vérifient chacune des deux équations. L'équation
$(x-3)^2+(y-3)^2-1^2=(12-0)(x-3)+(12-0)(y-3)$
est vérifiée par les coordonnées des points D et E, mais aussi par une infinité d'autres (c'est l'équation d'un cercle).
Donc seules les deux premières lignes sont bonnes, et il faut écrire le système de deux équations puis le résoudre.

Calcul de coordonnées