Graphique fonction cosinus et exercices

[josephinege]

Bonjour

J'ai cet exercice en 3 parties basé sur une fonction cosinus que je ne parviens pas à résoudre. Je bloque dès la première question , donc je n'ai pas tellement planché sur les deux autres. J'espère que vous pourrez m'aiguiller pour que je le comprenne

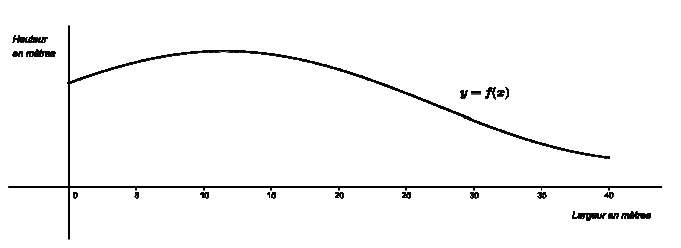
"Un étudiant en architecture a dessiné une façade en verre de 40 m de large en utilisant pour la partie supérieure le graphique de f(x) = 4 cos ( (x/10) -20) + 6

Aider cet étudiant à répondre aux questions suivantes en effectuant les calculs adéquats :
a) Quelle est la hauteur du point le plus élevé de cette façade ?
b) Combien mesure l'aire de cette façade, au mètre carré près ?
c) Sur quelle largeur, au cm près, cette façade mesure-t-elle au moins 6 mètres de haut ? "

Je vous joins le graphique ci dessous.

Merci beaucoup


-----

[gg0]

Bonjour.

A priori, si tu as cet exercice, c'est que tu connais la courbe de la fonction cosinus.
Mais déjà avec la courbe d'un cosinus, tu sais que le maximum pour un cos est 1, ce qui te donne le maximum de f(x) qui est ...
La question b est une application très simple des intégrales.
La dernière question se traite facilement en écrivant la condition (et en tenant compte de ce que x est compris entre 0 et 40).

Bon travail personnel !

[josephinege]

Effectivement cosinus(x) a un maximum égal à 1 quand x = 1. Donc quand ce qu'il y a entre parenthèse vaut 1 dans ma fonction, je me retrouve avec un maximum qui vaut 4 . (1) + 6 = 10 . Donc la fonction a pour maximum 10.

Ensuite pour la question 2 j'ai donc écrit que l'air valait l'intégrale de 0 à 40 de 4cos((x/10) -20) + 6

la primitive de la fonction vaut 4 ( sin ((x/10) - 20 ) + 6x ) . En appliquant le calcul avec les bornes j'ai obtenu 965 m²

Enfin pour la dernière question j'ai donc écrit 4 cos ((x/10) -20) + 6 supérieur ou = à 6. Donc cos ((x/10) -20) supérieur ou égal à 0.
Autrement dit (x/10) - 20 supérieur ou égal à pi/2 + kpi , donc x supérieur ou égal à 200+ 5pi + 10kpi
x supérieur ou égal à 215 + 10kpi , en sachant que k va de 0 à 5 pour respecter l'intervalle.

Pouvez vous confirmer mes calculs? Merci beaucoup d'avance

[gg0]

OK pour le début, mais ta primitive est fausse. D'ailleurs, 965 m² sur 40 m de large, ça fait une hauteur moyenne de plus de 24 m !! Tu aurais pu contrôler ton résultat.
Revois les primitives des fonctions de la forme f(ax+b) où f a une primitive connue. Ici, tu as 4 sin(1/10 x-20)+6 à intégrer. Tu fais aussi manifestement une énorme erreur de calcul en "appliquant le calcul avec les bornes". Combien vaut 4 ( sin ((x/10) - 20 ) + 6x ) pour x=40 ? (bien sûr, ça ne sert à rien pour l'exercice, mais je veux te faire voir ce que tu as vraiment fait)

Pour la dernière question, "cos ((x/10) -20) supérieur ou égal à 0" est correct, la suite n'a aucun sens. Regarde déjà dans quel intervalle varie t= (x/10) -20 quand x varie de 0 à 40; ensuite, regarde où est cet intervalle sur le cercle trigonométrique (-6 pi vaut environ -18,85 - t est un angle, plus précisément une mesure d'angle, donc se représente par un point du cercle).

Bon travail !

[A voir en vidéo sur Futura]

[ansset]

edit: inutile car pas vu le post précédent.

[josephinege]

Concernant tout d'abord le calcul "avec les bornes" que vous me demandez de refaire j'ai trouvé 243 est ce que c'est mieux ?

Enfin du coup concernant la résolution de l'exercice : ma primitive est donc mauvaise. J'ai appliqué le fait que u'.cos(u) a pour primitive sin (u) , ce n'est pas ce qu'il fallait faire ? Parce que dans ce cas là on peut faire apparaitre la dérivée de u, c'est à dire 1/10. On a alors pour primitive : 40 sin ((x/10) -20) + 6x . Ce n'est pas le même résultat que ce que j'avais écrit, j'ai donc du me tromper quelque part avant. Est cette fois ci la bonne réponse?

J'attends déjà votre réponse avant d'essayer de corriger mon résultat en ce qui concerne l'aire et la dernière question

Merci

[ansset]

c'est la bonne primitive.

[josephinege]

Ok donc en corrigeant mon intégrale j'obtiens une aire de 288 m².

Ensuite pour ce qui concerne la dernière question : quand x vaut 0 on ((x/10) -20 ) qui vaut -20 et quand x vaut 40 il vaut -16, il varie donc de -20 à -16 ? et cela se situe dans le quadrant 4 ?

[gg0]

Heu ... de -20 à -16, il y a une longueur de 4, donc plus d'un demi-tour. On est sur 3 quadrants, et on va regarder où le cos est positif.

[josephinege]

le cos est positif de 0 à pi/2 donc dans le quadrant 1 , non?

[ansset]

ramène toi au cercle trigo pour y voir plus clair.
que valent -16 et -20 dans le cercle trigo de base en rajoutant les 2pi*k qui vont bien.

[ansset]

le cos est positif de 0 à pi/2 donc dans le quadrant 1 , non?

le cos est positif entre -pi/2 et pi/2 ou de manière équivalente entre 0 et pi/2 et entre 3pi/2 et 2pi.
ici le plus simple est de se replacer entre -pi et pi.

[gg0]

Le cosinus est l'abscisse du point représentatif de x, donc quand ce point est dans la partie droite du cercle. Tu peux placer sur le cercle les points d'abscisse curviligne (suivant le cercle) -20 et -16 et repérer les points qui sont du bon côté, donc les nombres qui conviennent entre -20 et -16.