Exercice de Probabilités Conditionnelles avec un piège (TES)

[KOUKIA]

Bonjour à tous, Je vous écrit pour vous exposer mon problème:

Pendant les vacances nous devons traiter un Devoir Maison de mathématiques qui se compose de trois exercices. les deux premiers ne m'ont pas posé de soucis en revanche, le
troisième est bien plus compliqué, voici l'énoncé:

"Un vendeur propose ses produits soit en boutique,soit sur Internet.Il propose aussi une extension de garantie.
Ce vendeur constate que
-40% de ses clients achètent en magasin
-Les clients qui achètent en magasin se font souvent convaincre de prendre l'extension
de garantie:ainsi 80% de ceux-ci prennent l'extension de garantie.
-La proportion de ceux qui achètent en magasin et prennent l'extension de garantie est de 30%.
Pour un client pris au hasard,on notera les événements:
M: le client achète en magasin
I: le client achète sur internet
E: le client prend une extension de garantie.

"ATTENTION! il y a un piège"

Votre mission: un client à pris une extension de garantie, quelle est la probabilité qu'il ait acheté sur internet?

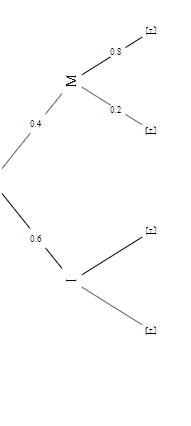
A vous de faire un arbre et de calculer ce dont vous avez besoin.

à présent je vais vous exposer ma démarche:

P(M)=0.4 donc P(I)=1-0.4=0.6
P(M inter E)=0.3
PE(M) ( probabilité de M sachant E) =0.80

Je fais l'arbre et il me manque P de E sachant M:

donc je fait P de E sachant M = P(M inter E)/P(M)=0.3/0.4=0.75
en fessant 1-0.75 j'arrive à déduire que P de E barre sachant M vaut 0.25
de même que P de E sachant I = 1-0.75 = 0.25
alors P de E barre sachant I vaut 1-0.25 = 0.75
j'en déduit que P(M inter E barre) =0.1
P(I inter E)=0.15
P(I inter E barre)=0.45
en fessant les probas totales on trouve P(E)=0.45 car P(E)=P(M inter E)+P(I inter E)
=0.30+0.15=0.45
Donc la réponse à la question est la suivante:
P(I sachant E)=P(I inter E)/P(E) = 0.15/0.45 = 0.33

Voici ou j'en suis pour l'instant je ne suis pas tout à fait sur si il y a du juste ou du faux mais je pense que le piège résidait dans ce fameux 80% trompeur qu'il ne fallait pas utiliser.
J'éspère que l'on va travailler ensemble pour résoudre cet exercice.

PS: dans l'arbre il y a E et E barre faites attention avec les 2 branches

Bien à vous,
Alexandre
-----

[ansset]

"Un vendeur propose ses produits soit en boutique,soit sur Internet.Il propose aussi une extension de garantie.
Ce vendeur constate que
-40% de ses clients achètent en magasin
-Les clients qui achètent en magasin se font souvent convaincre de prendre l'extension
de garantie:ainsi 80% de ceux-ci prennent l'extension de garantie.
-La proportion de ceux qui achètent en magasin et prennent l'extension de garantie est de 30%.

Est ce l'énoncé ?
j'ai l'impression qu'il y a un bug, entre les deux premières assertions et la troisième.
car 80% de 40% fait 32% et non 30%
qui serait le nb d'acheteurs en magasin prenant l'extension selon la troisième info, telle qu'écrite.

celle ci ne concernerait pas la proportion de clients Internet qui prennent l'extension ?

[KOUKIA]

Bonjour Monsieur, Merci vraiment de l’intérêt que vous porter à mon exercice en fait après avoir vérifié l'énoncé plusieurs fois j'ai écrit les données comme elles sont marquées dans l'énoncé donc je ne pense pas qu'il y ait d'erreur à moins que c'est le piège dont fessait allusion le professeur et si c'est le cas quand j'utilise 32% je n'arrive pas à répondre à la question surtout pour trouver ce qui me manque dans l'arbre.

[ansset]

je n'ai pas lu en détail tes calculs.
mais dans tous les cas , si tu n'as aucune information ( directe ou indirecte ) sur les les clients Internet prenant l'extension ( ou la prop totale de ceux qui prennent l'extension) , je ne vois pas comment tu peux résoudre ton pb.

[A voir en vidéo sur Futura]

[KOUKIA]

merci alors je pense que c'est dans votre dernière question que réside le piège je vais partir du postulat que les 30% concernent les clients d'internet ayant pris l’extension de garantie
et je confirmerais

[ansset]

dans ce cas , je n'appelle pas ça un piège, mais un énoncé "foireux".
le prof fait il des coups tordus comme ça ?

[ansset]

a noter qu'en prenant cette hypothèse, on trouve un % total de prise d'extension de garanti qui tombe "très rond" !

[KOUKIA]

Pour répondre à votre question je pense peut-être qu'il fait des énoncés foireux l'autre fois il nous à donné un DM sur les matrices ou il fallait manipuler une matrice ,
2x3 du nom de A et 2x1 du nom de B et de dire si AXB est possible ou BXA est possible en détaillant les calculs du produits que l'on peut faire ce qui est impossible et absurde car il faut que le nombre de colonne de la 1re matrice soit égal au nombre de ligne de la deuxième. néanmoins je tient à souligner le fait que pour réviser le baccalauréat il nous fais faire des exercices pas très communs.

[ansset]

alors, pars la dessus, et la solution tient en 2 lignes.
dis nous ce que tu trouves.

ps : dans tous les cas, présenté tel qu'au début, on ne peut conclure

[KOUKIA]

Très bien:
Je pars du postula que PI(E)=0.3 j'en déduis assez facilement que P(I inter E)= P(I)x PI(E)=0.6*0.3=0.18
J'applique la formule des probabilités totales:
P(B)=P(I inter E)+P(M inter E)=0.18+0.32=0.50
J'applique la formule de Bayes pour trouver PE(I) qui est la question de l'énoncé:
PE(I)=P(I inter E)/P(E)=0.18/0.50=0.36
La probabilité qu'un client ait acheté sur internet sachant qu'il a prit l’extension de garantie est de 0.36 soit 36%

[ansset]

idem pour moi.
en revanche je ne sais pas ce que tu as pu faire comme calcul initialement car il manquerait une donnée.

[KOUKIA]

je pense que sans votre remarque pertinente par rapport à ce "30%" l'exercice ne pourrait pas être résolu. Juste par curiosité êtes vous professeur de mathématiques?

[ansset]

Non, j'ai fait des études d'ingé, mais j'ai tj fait un peu "joujou" avec les maths . soit en donnant des cours à une époque, soit juste par plaisir.
ps: et professionnellement aussi ( dans la modélisation )