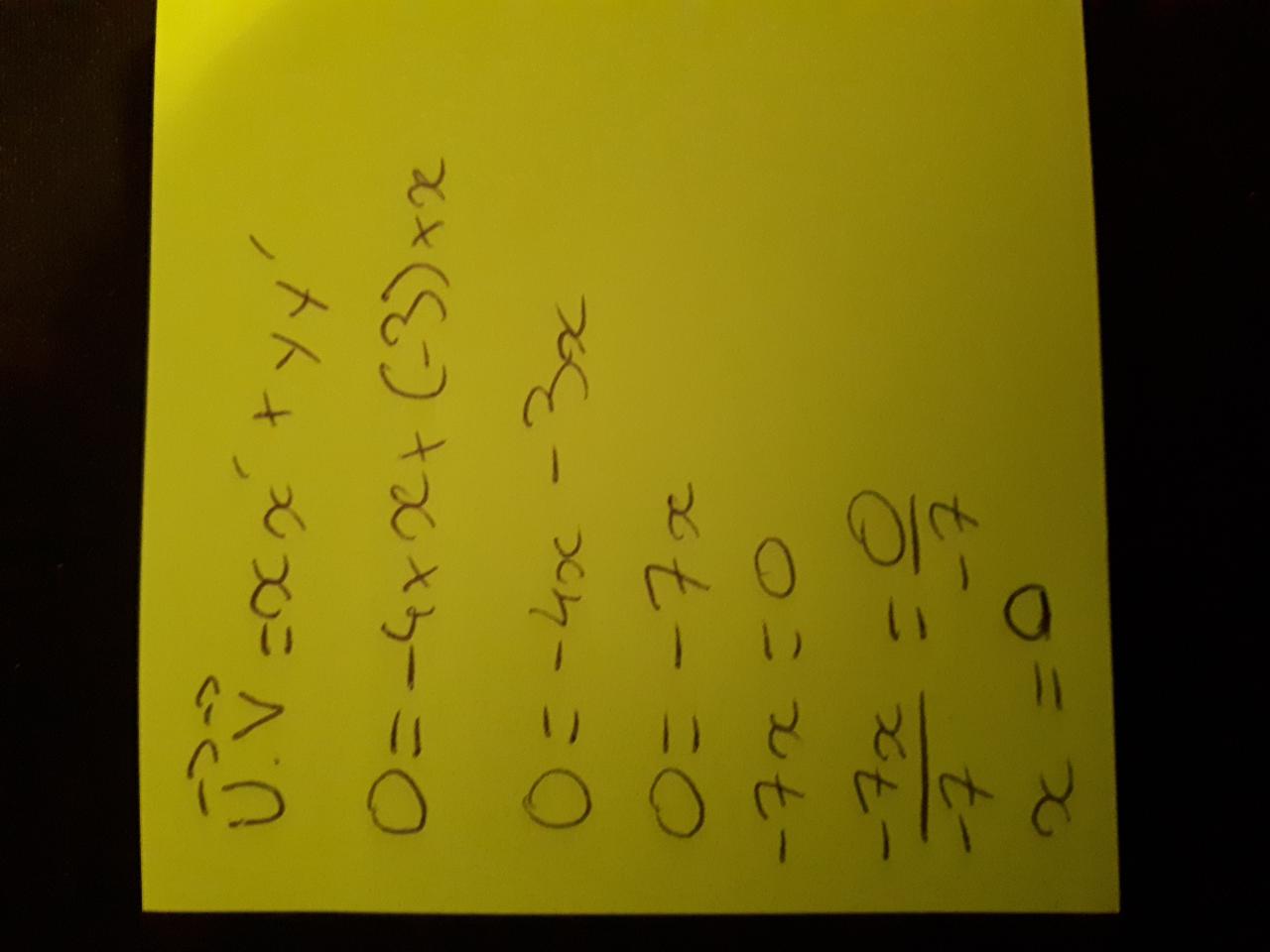Exercice produit scalaire
Discussions similaires
-
Par invite319b6bf6 dans le forum Mathématiques du collège et du lycée
Réponses: 6
Dernier message: 14/03/2015, 12h30
-
Par invited4743cb4 dans le forum Mathématiques du collège et du lycée
Réponses: 5
Dernier message: 14/05/2011, 17h56
-
Par invite086e3b29 dans le forum Mathématiques du collège et du lycée
Réponses: 3
Dernier message: 13/05/2010, 16h03
-
Par invite01e746e6 dans le forum Mathématiques du collège et du lycée
Réponses: 11
Dernier message: 16/02/2010, 12h36
-
Par invite6e80090c dans le forum Mathématiques du collège et du lycée
Réponses: 3
Dernier message: 01/09/2009, 10h32



 et
et