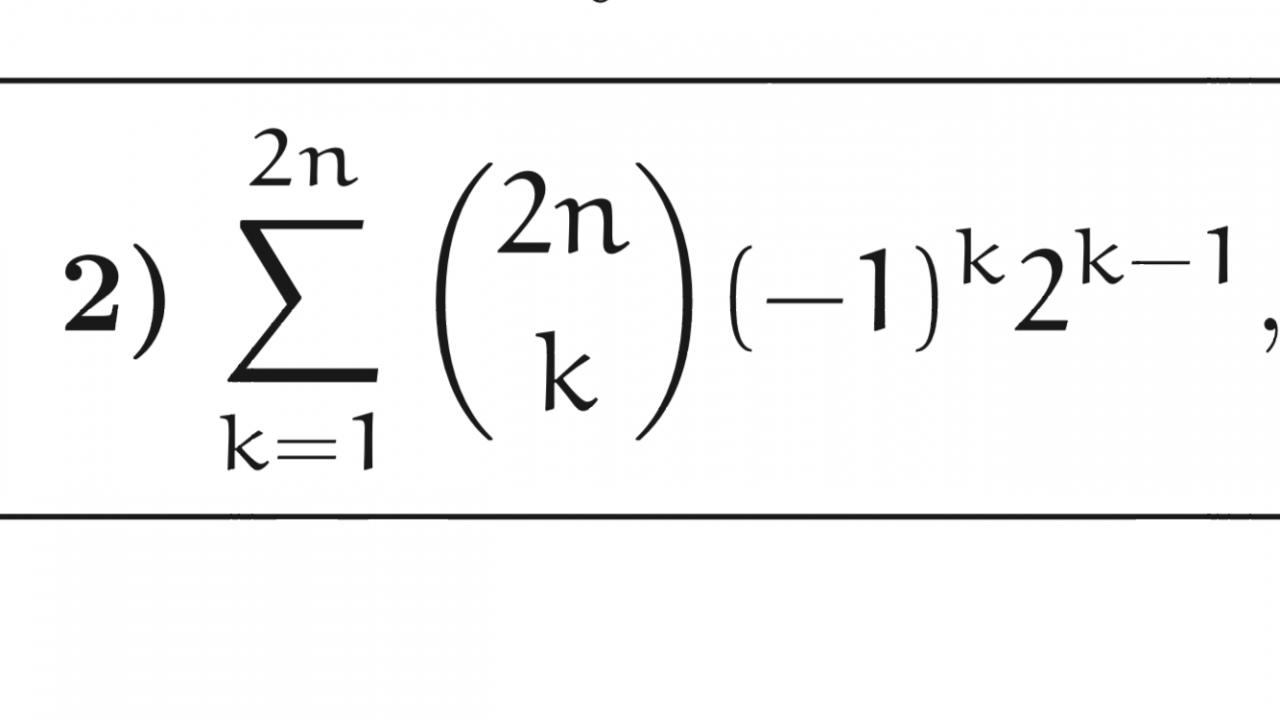Bonjour à tous ! J’essaye de faire des exercices sur les sigmas, et en particulier les exercices concernant le binôme début Newton. Et je n’arrive pas celui-là. Malgré la correction, je ne comprends pas les différentes étapes.
( je n’ai pas réussi à mettre les coefficients binomiaux en verticale mais entrée parenthèses ça correspond à la combinaison de k éléments parmi 2n.
Voilà j’espère que vous pouvez m’aider !
Merci d’avance
L'idée me semble t'il est de se rapprocher du développement binomial de (1 - 2)2n = 1.
Faut bricoler un peu et factoriser un chouya..
Dernière modification par jacknicklaus ; 05/05/2020 à 22h15.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Merci mais justement je n’arrive pas à faire ce petit bidouillage
Dans la correction ils arrivent à placer un 1/2 devant le sigma, mais je ne vois pas d’où il peut provenir.
C'est une technique classique : multiplier par (1/2)*2 et appliquer la distributivité pour rentrer le 2 dans la somme pour retrouver la formule. Autrement dit : On a besoin de multiplier par 2 à l'intérieur de la somme pour avoir la bonne puissance de 2, on le fait, ce qui multiplie toute la somme par 2, et on remultiplie par 1/2 pour que ce soit égal.
Cordialement.
Et ne pas oublier que la somme demandée va de k=1 à 2n, alors que le développement du binôme va de 0 à 2n... Donc classique, il suffit de dire (somme de k=1 à 2n) = (somme de k=0 à 2n) - (terme k = 0). Bon travail.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Donc, pour t'aider, complète cette (proposition de ) démarche : (j'écris avec des C(n,p) )
soit
Je posedéveloppement du binôme à compléter
or
d'où
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
