equation trigonométrique et racines

[invite8f16a957]

Bonjour,

Je bloque sur un exercice pourtant simple:

arctan(x)+arctan(2x)=pi/3

Pour le résoudre, j'injecte une tangente de part et d'autre de l'équation et obtiens:
tan(arctan(x)+arctan(2x))= racine de 3

Utilisant alors la règle "tan(a+b) = (tan(a)+tan(b))/(1-tan(a).tan(b))", j'obtiens:

1.jpg

Puis je cherche les racines:

2.jpg

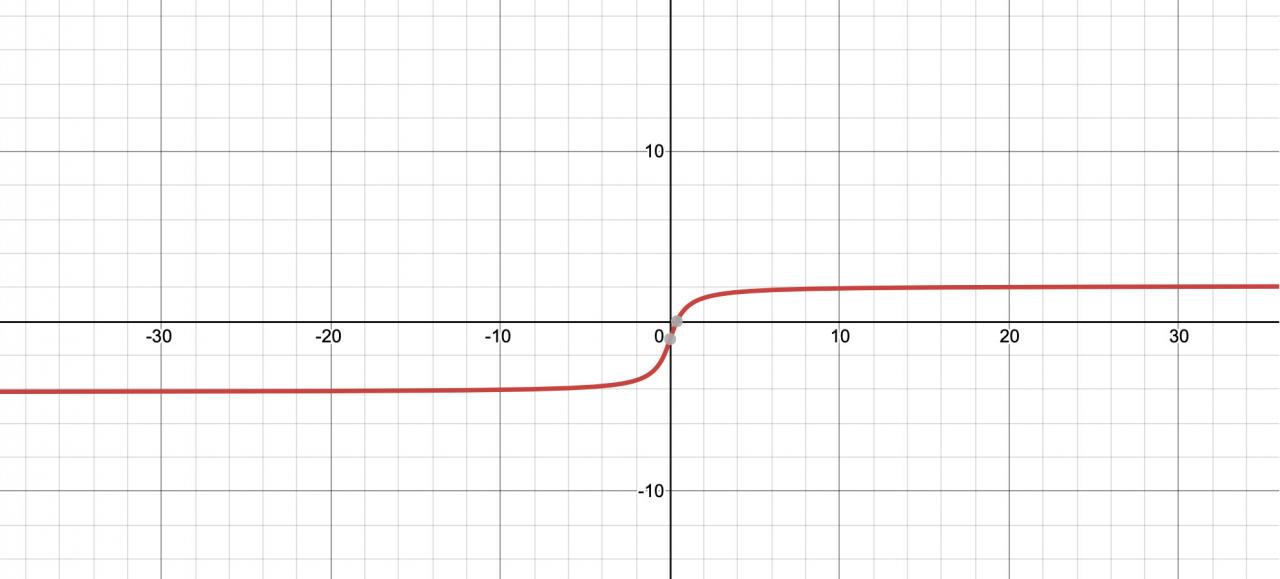
Or, j'ai cherché à vérifier mes réponses en ligne et quand je trace le graphique de cette fonction, j'obtiens;

Sans-titre-1.jpg

L'intersection avec l'axe des x est unique et la rencontre semble se faire à mon x1.

Et si je soumets l'équation en ligne sur un site qui donne les réponses, j'obtiens aussi une seule réponse qui correspond à mon x1.

J'ai pensé au fait que mon x2 est plus petit que -1 mais ça ne devrait pas être un souci puisque le domaine de x quand il s'agit de arctan(x) devrait s'étendre à tous les réels (contrairement à arcsin ou arccos).

Donc je ne vois pas mon erreur.

Merci pour votre aide.

PS: désolé, je ne sais ps du tout comment bien formater les maths sur ce forum.
-----

[jacknicklaus]

Donc je ne vois pas mon erreur.

normal, il n'y en a pas; ton x2 est une solution valide.

[invite8f16a957]

Ok merci mais alors pourquoi le graphe de la fonction ne reflète pas cette solution vu qu'il ne croise l'axe des x qu'en un seul point?

[invite8f16a957]

(Désolé, je ne vois pas de bouton pour éditer mes messages)

..et quand je plug le x2 dans l'égalité, elle n'est plus vérifiée.Je n'obtiens pas racine de 3.
De plus ce point existe parfaitement sur la courbe sans être pourtant une racine.
Jj'ai aussi utilisé une application en ligne qui résout les équations trigonométriques (afin de vérifier) et elle ne crache que mon x1, PAS le x2.
Ce qui tend à dire qu'il y a une bille dans le potage quand même, non?
Ce x2 est sensé être exclu pour une raison ou une autre et je ne sais pas pourquoi.
Il y a un truc qui me dépasse.

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

C'est la périodicité de tan qui te joue des tours. x2 correspond à Pi/3-Pi.

Cordialement.

[invite8f16a957]

Ah! Là je vois effectivement la lumière au bout du tunnel ! Merci ! Ca doit être ça.

Mais je ne comprends toujours pas le fond du problème. En tout cas graphiquement.
En effet, x2 correspond à -1 et des poussières. Or sur le graphe, ce -1 et des poussières sur l'axe des x correspond bien à un point du graphe sur cette période-ci (pi/3). Pas une autre



Donc je ne vois ni algébriquement, ni graphiquement comment prévoir que mon x2 ne peut être une solution viable.
Je l'admets volontiers car je sais que vous en savez plus que moi, mais j'aimerais surtout comprendre pour pouvoir le repérer à l'avenir sans quoi je ne vois pas comment ne plus faire l'erreur.

En bref: que manque-t-il dans ma résolution algébrique ci-dessus qui disqualifie explicitement x2?

[invite8f16a957]

Voici deux screenshots qui permettent d'expliquer ma confusion:

x2 donne ceci:

pic0.jpg

Or voilà où se trouve ce point sur le graphe qui ne sort ni du domaine ni de l'image ni ne se trouve sur une courbe d'une autre période:

pic1.jpg

Sur quelle base puis-je donc exclure ce x2 de mes solutions sans être péremptoire (et en connaissance de cause)?
Si mon calcul est formellement juste et que ce nombre apparait bien comme racine, q'est-ce qui, dans le calcul ou le graphe me permet de savoir que cette solution appartient à une autre période et est donc à exclure ?

Je sais, je me répète mais j'essaye de faire comprendre que je remets pas vos compétences en question, juste que les réponses, même si elles m'apportent énormément, ne me permettent pas (encore) de faire tilt.

[gg0]

Pour l'instant, je n peux pas voir tes pièces jointes ("en attente de validation"). Alors juste quelques remarques :

* le passage par tan ne donne pas une équation équivalente. Donc la seule chose qu'on sait est que si x est une solution, alors il vérifie l'équation et vaut x₁, ou x₂, ou les deux. Il reste, comme d'habitude quand on traite une équation par implication, à vérifier quels sont, parmi les nombres trouvés, ceux qui conviennent.
* la fonction x--> arctan(x)+arctan(2x) est de façon évidente impaire, croissante et positive seulement sur R+. Donc une éventuelle solution négative est à rejeter. Reste à vérifier que x₁ est solution.
* Cette fonction étant continue et variant de -Pi/2 à Pi/2 (exclus) prend toute valeur intermédiaire une fois et une seule. Donc il y a bien une solution. C'est x₁.

Cordialement.

[invite8f16a957]

Génial !

Le deuxième point de ta démonstration a été une illumination car il me permet de pouvoir anticiper le problème les prochaines fois. Je n'ai pas du tout pensé à voir l'incidence de la parité et de la croissance sur le domaine de la fonction dans mes résultats. C'est ce genre d'Eureka! que je cherchais.

En attendant, j'avais posé la question sur un forum anglo-saxon et, pour ceux qui comprennent, la dernière réponse est très éclairante car la personne explique graphiquement pourquoi le x2 EST et n'est PAS une solution valide, selon le point de vue. j'ai enfin pu voir pourquoi mes deux x restaient des points remarquables.

https://math.stackexchange.com/quest...570977_3683868


Merci beaucoup !