Bonjour à toutes et à tous.
J’ai voulu, comme cela, pour m’amuser, vérifier la validité d’un intervalle de confiance à 95 % sur un grand nombre de lancers de dés.
Pour ce faire j’ai simulé 10 000 lancers de 1000 dés.
Pour chacun des lancers de 10 000 dés, j’ai calculé la moyenne ainsi l’intervalle de confiance à 95 % centré sur la moyenne.
Comme on le sait, la moyenne des points sur un dé est de 3,5.
Bon après je regarde sur les 10 000 intervalles de confiance « combien encadrent correctement la « vraie » moyenne de 3,5 » ?
Je trouve qu’environ 95 % des intervalles des confiance encadrent correctement la vraie moyenne, et que dans seulement 5 % des cas la vraie moyenne est en dehors de l’intervalle.
Ouf. Tout va bien.
Puis je me demande : « que se passe t’il si je diminue le nombre de lancers de dés » ?
D’un côté, avec moins de dés, la dispersion des 10 000 moyennes calculées sera plus grande, donc on pourrait se dire que plus de moyenne vont statistiquement « sortir » de l’intervalle de confiance.
Mais d’un autre côté, étant donné que dans le calcul de l’intervalle de confiance, on divise par racine de N (le nombre d’échantillons), plus N est petit, plus l’intervalle de confiance s’agrandit.
Je pensais que ces deux effets se compensant, on aurait certes des intervalles de confiance de plus en plus larges à mesure que N diminue, mais qu’on aurait toujours 95 % de « bons encadrements ».
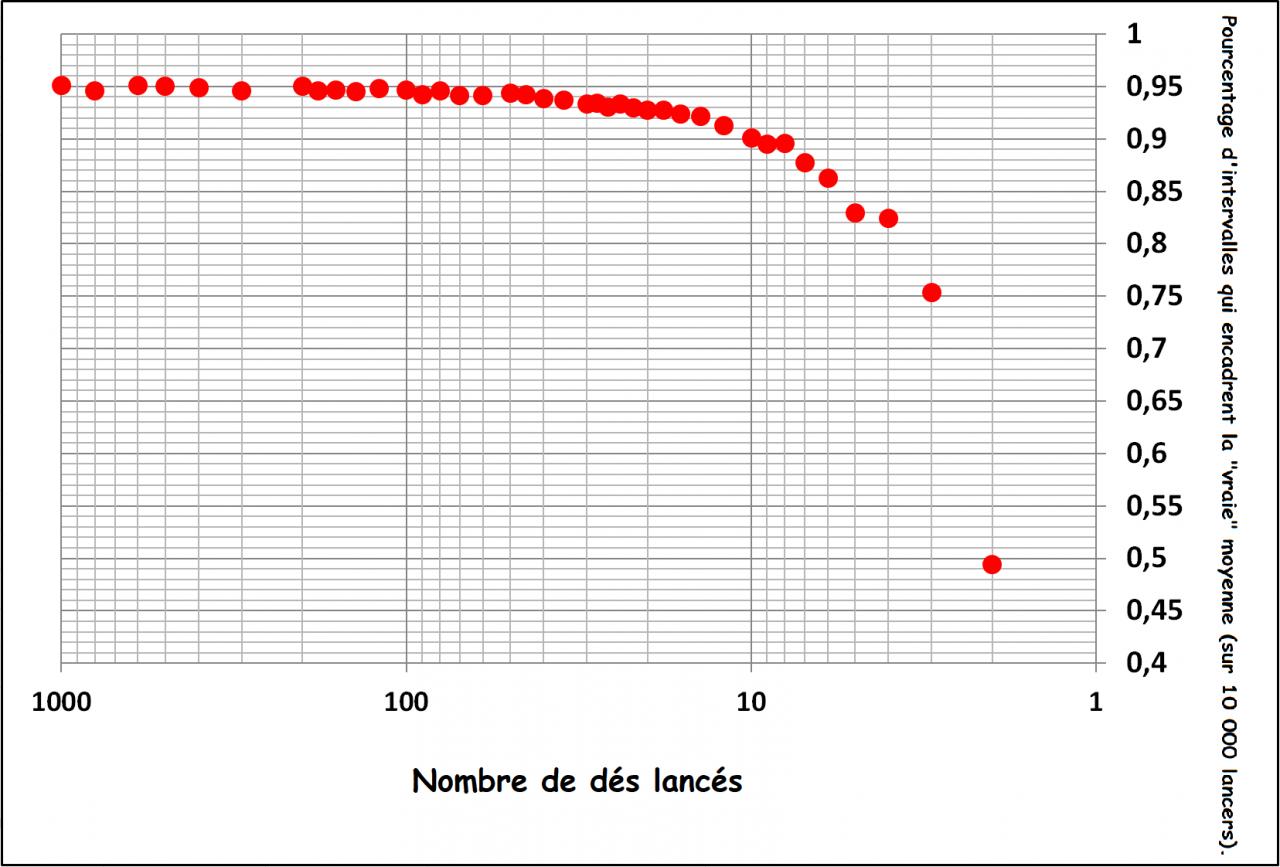
Alors oui on a bien des intervalles de confiance de plus en plus élargis, mais regardez ce qu’il se passe quand je regarde le pourcentage de « bons encadrements » de la vraie moyenne (3,5) en fonction du nombre de lancers de dés :
Comment expliquer cette dérive ?
-----