Fonction exponentielle exercice

[Lachimiecphysique]

Bonjour, j’ai besoin de votre aide pour l’exercice suivant:
On souhaite étudier la suite (U_n) définie par U₀= a et où pour tout n appartenant à N on a U_n+1= e^2Un- e^Un. On précise que cette égalité peut s’écrire de la façon suivante: U_n+1 = e^Un(e^Un-1) et que a est un nombre réel fixé non nul.

Questions:

1) On suppose que a <= 0. Démontrer par récurrence que, pour tout entier naturel n que U_n<= 0
2)a)Soit la fonction g définie pour tout réel x par : g(x) = e^2x- e^x- x. Calculer g’(x) et prouver que, pour tout réel x: g’(x) = (e^x-1) (2e^x+1)
2)b) Déterminer les variations de la fonction g et donner la valeur de son minimum.
2)c) En remarquant que U_n+1- U_n = g(U_n), montrer que la suite (U_n) est croissante.
3)a) On suppose maintenant que a > 0, la suite (U_n) étant croissante d’après la question précédente, on peut affirmer que pour tout entier naturel n, que u_n>= a. Essayez de démontrer que pour tout entier naturel n on a U_n+1- U_n >= g(a)
3)b) Démontrer par récurrence que pour tout entier naturel n, on a U_n>= a + n * g(a)

Mes réponses :

1) Soit la suite (U_n) définie par U₀ = a et pour tout n appartenant à N par U_n+1= e^2Un-e^Un

Démontrons par récurrence que pour tout entier naturel n, Un >= 0

Initialisation :

On suppose que a <= 0, donc U₀<= 0
Ici l’initialisation est vérifié car U_n<= 0.
Donc la propriété est vraie pour n=0

Hérédité :
Supposons qu’il existe un entier k tel que la propriété soit vraie pour U_k<= 0

Démontrons que la propriété est vraie au rang k+1 soit U_k+1<= 0

Donc si U_k<= 0
U_k* (e^2Uk- e^Uk) <= 0*(e^2Uk- e^Uk)
U_k * e^Uk(e^Uk-1) <= 0
Alors (U_k*e^Uk(e^Uk-1))/U_k<= 0/U_k
e^Uk (e^Uk-1) <= 0
Donc on peut dire que U_k+1 <= 0

Conclusion : Cette propriété est vraie pour n=0 et héréditaire à partir de ce rang, donc elle est vraie pour tout n appartenant à N

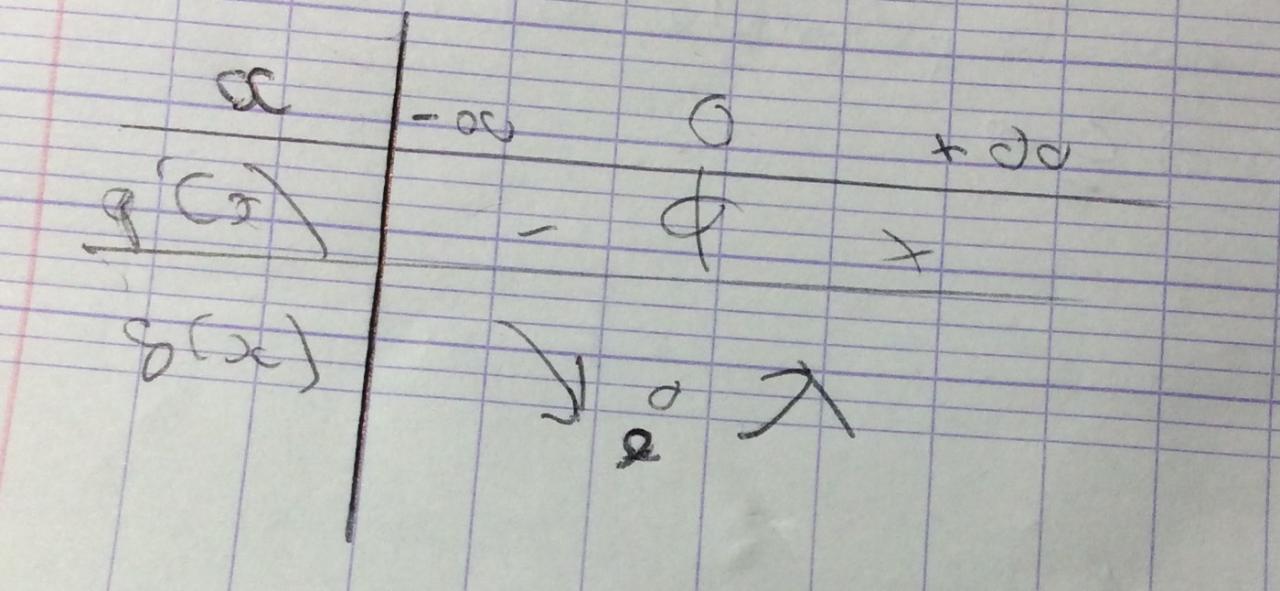
2)a) Soit g(x) = e^2x- e^x-x
donc g’(x) = 2e^2x- e^x-1
= 2e^2x+ e^x-2e^x-1
= e^x*2e^x+ e^x - 2e^x-1
= (e^x-1)*(2e^x+1)


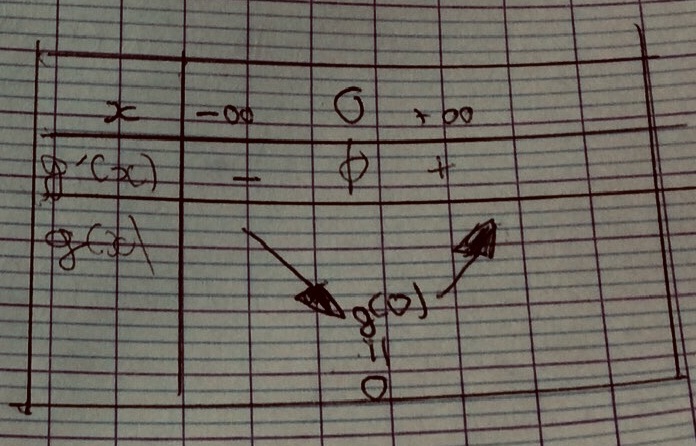
2)b)Déterminons les variations de g et donnons la valeur de son minimum :
*(2e^x+1) sera toujours positif pour tout x appartenant à R
*Pour (e^x-1) on a g(0) =e⁰ - 1 = 1-1=0
Donc g(x) est décroissant sur ]-oo;0[ et croissant sur ]0; +oo [

2)c) On sait que g(U_n) = e^2Un- e^Un- x

Où U_n+1- U_n= e^Un(e^Un-1) - U_n
= e^2U_n - e^U_n - U_n
= ? (Par quoi doit-on remplacer U_n pour trouver g(x) à travers U_n+1- U_n ?)

3)a) ?
3)b) ?


Merci si vous pouvez m’aidez, bonne journée
-----

[gg0]

Bonjour.

Ta rédaction pour la récurrence est de la haute fantaisie.
Je passe sur l'erreur de début ("Démontrons par récurrence que pour tout entier naturel n, Un >= 0" erreur de copie); mais la partie hérédité est absurde : pourquoi calculer U_k* (e^2Uk- e^Uk) qui n'a pas grand chose à voir avec U_k+1 ? et à la fin, tu nous sors la bonne inégalité par un tour de passe passe, une tricherie sur la division par u_k (comment fais-tu si u_k=0 ?), division par un nombre négatif !! Mais déjà à la première ligne tu trichais avec les règles de manipulation des inégalités (d'ailleurs comme (e^2Uk- e^Uk) est négatif, par hypothèse et U_k aussi, U_k* (e^2Uk- e^Uk) <= 0 est une énorme erreur.

A toi de reprendre cette preuve en utilisant vraiment l'énoncé, et en appliquant les règles sur les signes et manipulations d'inégalités.

Cordialement.

[Lachimiecphysique]

Bonjour merci pour votre réponse , j’avoue avoir dû mal de lier à la fois la fonction exponentielle et la récurrence, j’ai essayer de nouveau quelque chose pour l’hérédité mais je pense que ça va être de nouveau absurde...

U_k<=0
donc U_k+e^2Uk<= 0 + e^2Uk
U_k+ e^2Uk- e^Uk <= e^2Uk - e^Uk
Donc e^2Uk- e^Uk <= e^2Uk - e^Uk-U_k
Donc U_k+1 <= (e^2Uk- e^Uk) - U_k

Vu que (e^2Uk- e^Uk) est négatif par hypothèse et qu’on suppose U_k <= 0, on peut donc déduire que U_k+1<=0...

Merci si vous pouvez me donner un indice

[gg0]

"Vu que (e^2Uk- e^Uk) est négatif par hypothèse " !! Non, ce n'est pas l'hypothèse de récurrence, c'est ce que tu dois démontrer !

Tes deux tentatives n'utilisent jamais (sauf accessoirement) le fait que U_k+1 = e^2Uk- e^Uk. tu peux remplacer à chaque fois e^2Uk- e^Uk par n'importe quelle expression en fonction de U_k, par exemple sin(U_k) ou (U_k)², ça marche de la même façon. C'est à dire que ce n'est pas une preuve (avec U_k+1 = (U_k)², tu auras du mal à prouver que c'est négatif !!!).

Donc il va falloir travailler avec l'expression de U_k+1, l'obtenir négative à partir de U_k, et sans tricher. Tu as une indication dans ton énoncé, elle permet (connaissant les propriétés de l'exponentielle) d'y arriver en 3 lignes.

A toi de faire ...

[A voir en vidéo sur Futura]

[Lachimiecphysique]

Bonjour merci pour votre réponse.
Je vais être honnête avec vous et malgré votre explication , je ne comprends toujours pas la démarche...
Je sais que l’indication dans l’énoncé est que U_n+1= e^2Un - e^Un peut s’écrire U_n+1= e^Un (e^Un-1) mais je ne vois pas malheureusement l’utilité de ceci ...
Sinon voici les propriétés de l’exponentielle que je connais par image

Merci si vous pouvez juste détailler la 1ère ligne du calcul, désolé d’abuser

[gg0]

Bon, je vais te faire l'exercice, puisque tu ne veux pas t'attaquer à l'expression . Tu n'as jamais essayé de sérieusement prouver que ce produit est négatif; pourtant les cours sur le signe d'un produit, c'est du collège, et souvent utilisé depuis !
Tu as oublié une propriété très utile de la fonction exponentielle : Elle est croissante.

Donc

A partir de l'hypothèse de récurrence on déduit

puis par multiplication par un nombre positif

c'est à dire


Tu remarqueras que j'ai bien utilisé l'expression de u_n+1 en fonction de u_n pour prouver. En elle-même.

Il te reste maintenant à
* refaire correctement la question 2-b (tu ne réponds pas à la question et il y a une ligne "*Pour (e^x-1) ..." qui n'a aucun sens, et les sens de variation ne sont pas justifiés.
* reprendre la question 2-c en calculant correctement g(u_n)
* puis faire la suite, qui n'est que l'utilisation de (j'espère que tu sais le démontrer)

NB : ton énoncé est un peu bizarre ("On suppose maintenant que a > 0, ... d’après la question précédente" alors que la question précédente supposait )

Cordialement.

[Lachimiecphysique]

Bonsoir merci pour votre aide, voici ce que j’ai fais grâce à votre calcul pour l’hérédité du 1):

Donc si U_k <= 0
Alors e^U_n<= e⁰
e^U_n <= 1
e^U_n-1 <= 0
e^U_n*(e^U_n-1) <= 0*e^U_n
Donc e^U_n(e^U_n-1) <= 0
On en déduit donc que U_k+1<= 0

Ensuite pour le 2)b) j’ai fais la chose suivante:

*(2e^x+1) sera toujours positif pour tout x appartenant à R
*Pour (e^x-1) on a e^x-1 = 0
où e^x = 1
e^x=e⁰
Alors x=0
On a donc un minimum en x=0

Voici le tableau de variations:



c) Un+1 - Un = e^Un(e^Un-1) - Un
= e^2Un - e^Un - Un
= g(Un)

Vu que e^2Un- e^Un> 0 la suite (Un) est donc croissante.Cela suffit-il comme réponse ?

3) ?

Merci pour votre aide

[gg0]

Pourquoi après avoir pris U_k <= 0 il y a des n, et plus de k ?

Pour le 2 b tu ne justifie nulle part le signe de g'(x). Savoir que g(x) vaut 0 pour x=0 ne donne pas son signe (0 est le seul cas où le signe est à la fois + et -, mais ailleurs ?).

Le c est du n'importe quoi ! Tu te moques du monde. Tu as mis 2 jours pour écrire une preuve que e^2Un- e^Un est négatif et tu viens écrire "Vu que e^2Un- e^Un> 0". Tu as la mémoire d'un cactus ??? Et en plus ça n'a aucun rapport avec ce qui précède !
Je crois que je vais arrêter de t'aider, tu n'utilise même pas 1% de ton cerveau, juste la partie qui guide la main ...

[Lachimiecphysique]

Bonsoir désolé de répondre que maintenant et de vous avoir mis en colère, croyez moi, j’utilise 100% de mon cerveau mais il ne correspond même pas à 1% du vôtre .

Je vous mets ci-joint ce que j’ai fait:

2)b) Déterminons les variations de la fonction g et donnons la valeur de son minimum:
*(2e^x+1) sera toujours positif pour tout x appartenant à R car on aura toujours e^x>0
*Pour (e^x-1) : e^x-1=0
<—> e^x-1 =0
<—> e^x= e⁰
Donc x =0

On a donc la possibilité de déterminer le tableau de signe ci-dessous:
Pièce jointe 422045

En conséquence, il est possible de déterminer le tableau de variations ci-dessous pour la fonction g:



2)c) On sait que U_n+1= e^U_n(e^U_n-1)
Donc U_n+1- U_n = e^U_n(e^U_n-1) - U_n
= e^2U_n- e^U_n-U_n

On sait que g(x)= e^2x- e^x -x, donc g(U_n) = e^2U_n- e^U_n - U_n
Alors U_n+1 - U_n = g(U_n)

Grâce au tableau de variation précédent on sait que g(x) est toujours >= à 0 (où g(0)=0 est le minimum), on en déduit donc la même chose pour g(U_n).

Donc U_n+1 - U_n = e^U_n- e^U_n - U_n
Où g(U_n)>0, la suite (U_n) est donc croissante .

3)a) *On sait que U_n est supérieur ou égal à a pour tout entier naturel n.
*U_n+1= e^U_n (e^U_n-1)
Donc U_n+1 = e^a (e^a-1)
= e^2a- e^a

Alors on a U_n+1 - U_n >= e^2a - e^a - a
Donc U_n+1 - U_n >= g(a) pour tout entier naturel n

b) Soit (U_n) la suite définie par U₀ = a et pour tout entier naturel n par U_n+1 = e^2a- e^a

Démontrons par récurrence que U_n >= a + n * g(a)


Initialisation:

Pour n=0, U₀ >= a + 0 *g(a)
donc U₀ >= a
En sachant que U₀ = a, l’initialisation est vérifiée car a >= a
La propriété est donc vraie pour n=0

Hérédité
Supposons qu’il existe un entier k tel que la propriété soit vraie: U_k >= a + k *g(a)

Démontrons que la propriété est vraie au rang k+1 , soit U_k+1 >= a + (k+1) *g(a)

Donc U_k >= a+k*g(a)
(Je pense avoir triché ici ...) Pour tout entier naturel n on a U_k supérieur ou égal à a
Donc a >= a + k * g(a)
Donc a +(k+1) >= a + k * g(a) +(k+1)
Donc a + (k+1) *g(a) >= a+k*g(a) + (k+1) *g(a)
Alors U_k+1 >= a + k * g(a) + (k+1) *g(a)
On en déduit donc que U_k+1>= a + k * g(a)

Conclusion:

Cette propriété est vraie pour n=0 et héréditaire à partir de ce rang, donc elle est vraie pour tout entier naturel n.

Merci beaucoup si vous avez encore le courage de m’aider !

[gg0]

Toujours pas d'étude du signe de g'(x) !! Ce que tu as fait s'applique parfaitement à g'(x)=(2e^x+1)(1-e^x) qui a pourtant le signe contraire. Savoir que (e^x-1) s'annule pour x=0 ne dit pas si (e^x-1) est positif ou négatif ailleurs : Tu écris bêtement par habitude - d'abord, + après, ou tu triches (tu as regardé la courbe de g).
La 2c mériterait l'élimination du baratin inutile à la fin pour dire ce qui compte vraiment : U_n+1 - U_n >= 0 (et g(x)>0 est faux !!!)

3 b : l'initialisation est une énormité logique : Tu dois démontrer U₀ >= a + 0 *g(a), et tu commences par l'affirmer !!! pour arriver à une propriété vraie, ce qui ne prouve rien !!!
On ne t'a jamais appris que la conclusion vient à la fin ? Même en français !!
Ne jamais commencer par le conclusion, c'est absurde.

Pour la suite, tu as effectivement triché. Donc tu n'aurais jamais dû écrire cela. Tu as remplacé U_k par a. Pourtant U_k ce n'est pas a. Donc tu savais que c'était une tricherie, mais tu l'as écrit quand même !! Arrête ce genre de comportement, sinon je vais penser que ce n'est pas 1% de mon intelligence, que tu as, mais 0%.

En fait, tu as beaucoup plus d'intelligence que tu ne crois, mais (au moins en maths) tu l'économise fortement : Tu utilise ta mémoire pour imiter, mais tu ne te fatigues pas à comprendre, à relier les idées (par exemple ici, l'hérédité est une conséquence immédiate de la question précédente), à contrôler que tu appliques bien des règles mathématiques. Dommage !

[Lachimiecphysique]

Bonjour, désolé de répondre que maintenant. Je vais arrêter de vous demander de l’aide pour cette exercice et je vais essayer de le finir seul avec les indications que vous m’avez donné.
Merci pour tout, bonne journée.