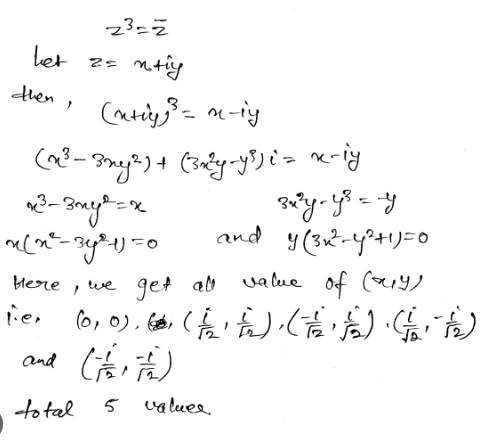resoudre dans C: z³=z conjugé

[ahmadhh]

Bonjour!

Donc, pour resoudre cette equation, doit on utiliser la methode traditionnelle pour resoudre les equations des nombres complexes; càd prendre z = a+bi (et z conjugé=a-bi) et proceder par (x+iy)³=x-iy, ou par contre utiliser la formule de moivre; càd:
on prends z=r.e^(iθ):

ma question la c'est pourquoi a-t-on ajouté "2kπi" en passant de la 1ere expression à la 2eme, et comment a-t-on deduit les 5 solutions juste à partir de l'expression θ=kπ/2

ce que j'ai remarqué aussi c que les deux methodes donnent des resultats differents (ms toujours 5 solutions)

merci

-----

[gg0]

On n'a pas "ajouté "2kπi" ", mais appliqué la règle sur l'égalité de deux complexes donnés sous forme exponentielle. Revois le cours.

Quant au fait que les méthodes donnent des résultats différents, c'estpeut-être normal, ce que tu as repris ci-dessus est très incomplet :



on en déduit deux équations :


La première équation donne r=0 ou r=1 ou r=-1 (exclu puisque le module est un nombre positif)
Le cas r=0 a été oublié !

Cordialement.

Au besoin, expose l'autre méthode, on regardera, mais les 4 solutions proposées doivent apparaître, plus z=0.

[ahmadhh]

On n'a pas "ajouté "2kπi" ", mais appliqué la règle sur l'égalité de deux complexes donnés sous forme exponentielle. Revois le cours.

tout de suite

Quant au fait que les méthodes donnent des résultats différents

voici un example de la 1ere methode, qui donne des resultats totalement differents

on en déduit deux équations :

merci bcp pour mentioner ce point là

[ahmadhh]

aussi j'ai une petite question hors sujet: si on a arg(z)=8π[2π], est-ce cela equivaut à arg(z)=0[2π]
et la forme trigo reduite, serait-elle comme cela: z=[1;0]

[A voir en vidéo sur Futura]

[gg0]

message #3 : A part (0,0) les couples solutions ne sont pas des valeurs admissibles pour x et y (qui sont des réels). Et si on prend x=0, solution de la première équation, la deuxième équation donne d'autres solutions pour y que 0. Fais le calcul ...
message #4 : Bien sûr, le [2π] veut dire qu'on peut ajouter ou soustraire autant de fois 2π que l'on veut pour obtenir un des nombres évoqués.
x=a [2π] signifie x=a +k 2π avec k entier relatif.

[ahmadhh]

les couples solutions ne sont pas des valeurs admissibles pour x et y

donc cela veut dire que cette methode n'est pas valable

merci encore

[gg0]

Si !

En résolvant correctement, on trouve comme couples solutions (0,0), (0,1), (0,-1), (1,0) et (0,1), qui donnent les 4 solutions du message #1 plus la solution oubliée z=0.

[ahmadhh]

impeccable, merci