Approximation de fonction trigonométrique

[Lzfix]

Bonjour à tous,

Je vais essayer d'expliquer clairement mon questionnement bien que cela soit un peu flou pour moi pour le moment. (je ne sais pas si je suis dans le bon sous-forum, mais j'estime que cela reste des mathématiques du lycée ?).

Pour donner un peu de contexte :
Je suis tombé sur un problème qui consiste à calculer l'aire d'une figure. Dans un triangle équilatéral, tracer un cercle en chaque sommet passant par le milieu des côtés adjacents (soit 3 cercles). L'aire de la figure correspond à la soustraction des morceaux de cercle du triangle (surface en rose) :
Figure.PNG

Suite à cela j'ai réaliser une généralisation pour chaque polygone régulier et tracé sur excel la courbe d'évolution de cette surface en fonction du nombre de côté.
Je précise que j'ai réalisé tous les calculs par rapport à :
r - le rayon des cercles (qui vaut 1/2 du côté du polygone)
θ - l'angle interne du polygone régulier (si on trace n triangles isocèles, c'est l'angle opposé au côté du polygone)
Figure 2.PNG

J'en arrive à une formule (honnête) du style : A = R²( (n/tan(π/n)) - (π(n-2)/2))

Après traçage de la courbe sur excel et un peu de courbe de tendance, il semblerait qu'il soit possible d'approximer (de manière très proche quand n tend vers l'infini) : A = (n²/π - n(π/2) + 2π/3).

Ce qui me rend très confus quand à pourquoi ?
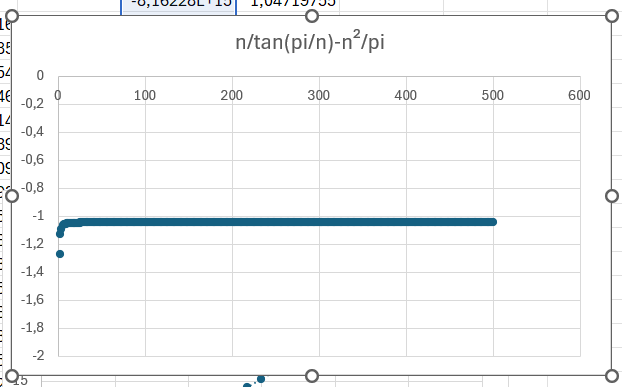
Ma question est donc comment peut-on retrouver l'approximation pour n tendant vers +∞ de : n/(tan(π/n) = n²/π - π/3

Si on étend au première ordre 1/tan(π/n) on trouve qqc du genre n/π, ce qui amène vers le terme n²/π mais je ne comprends pas d'où sort le π/3. Je n'ai pas les outils mathématique pour trouver ce résultat et je fonctionne par intuition / calcul de valeurs numériques.

Si qqn a des pistes ?

(je sais que c'est peut-être un peu fouilli désolé)
Bonne journée,
-----

[mach3]

pour les petits angles (exprimés en radians bien-sûr), on a
Quand votre n devient grand, votre angle devient très petit et donc

L'approximation vient de ce qu'on appelle un développement limité : https://fr.wikipedia.org/wiki/D%C3%A...nt_limit%C3%A9

m@ch3

[Lzfix]

Merci pour votre réponse, pour l'approximation pour les petits angles j'avais. Ce qui me parait étrange c'est que si on trace le graphe (pour les entiers positifs) de :
n/(tan(π/n) -n²/π on obtient cette figure :


On observe clairement un asymptote à 1.04... ce qui correspond presque (en fait je suppose même que c'est égal quand je calcul pour n=100000 la différence sur excel est nulle) à π/3.

Ce que je n'arrive pas à expliquer.
pour moi quand n tend vers l'infini on a :
n/tan(π/n) => n/(π/n) => n²/π. sachant que ce n'est que le premier ordre je m'attends à ce qu'il y est un différence qui évolue, mais elle reste stable à une valeur de -π/3

Ce qui me fait conclure qu'une approximation correcte est :
n/tan(π/n) = n²/π - π/3

Bonne journée,

EDIT :
Je viens de voir sur wolfram alpha que l'expansion en série de Laurent (que je ne connais pas du tout) équivaut : n²/π - π/3 - d'autres termes de rang supérieur. si je m'arrête à ces premiers termes, je retombe bien sur ce que mes errances m'ont amenées à trouver.
par contre je ne sais pas du tout d'où sort cette série (je n'ai pas très bien compris la fiche wikipedia de cela mais bon)

[mach3]

désolé, j'ai répondu à côté, je n'avais pas bien vu cette histoire de pi/3. Je ne comprend pas d'où il sort...

m@ch3

[A voir en vidéo sur Futura]

[Lzfix]

Ahah pas de soucis, je vais explorer ça de mon côté alors !

[gts2]

Bonjour,

désolé, j'ai répondu à côté, je n'avais pas bien vu cette histoire de pi/3. Je ne comprend pas d'où il sort...

Ce n'est pas à côté, c'est bien la bonne piste, il faut simplement passer à l'ordre suivant :


Pour @Lzfix : developpement-limite-de-tan-x-en-0

[mach3]

ok! Le fait qu'il y ait du n² en numérateur de la fraction fait qu'on ne peut pas négliger le terme en (pi/n)^3 du développement de tan(pi/n) au dénominateur, c'est ça?

m@ch3

[Lzfix]

Bonjour,

Merci pour ce retour, le problème que est que je suis pas très bon pour manipuler des séries de taylor.
De plus quand je passe de tan(π/x) à 1/tan(π/x) je suis perdu. aussi je regarde mon approximation pour x > 2 car entre 0 et 2 la fonction oscille et n'a pas un comportement utile dans mon cas.

Même en prenant un terme supplémentaire dans le développement de la série de taylor je ne vois pas comment retomber sur x²/π - π/3

[gts2]

Je préfère travailler avec les limites en zéro, je pose n=1/x devient donc

[Lzfix]

Oulah my bad j'ai mal vu, je vais reprendre ça plus sérieusement !

Mais merci pour l'astuce du changement de variable
aussi cette étape reste nébuleuse dans ma tête (voir la photo)

[gts2]

Ce n'est pas des maths de lycée mais de tout début de L1.

Vous dites "Je n'ai pas les outils mathématique pour trouver ce résultat et je fonctionne par intuition / calcul de valeurs numériques." donc je ne sais trop par quel bout le prendre.

Numériquement tracer 1/1+x et 1-x au voisinage de x=0
Mais vous parlez de Taylor, soit la fonction f(x)=1/(1+x) ; pour x petit, f(0) vaut 1 et f'(0) vaut -1 ce qui donne

[gg0]

Bonjour Gts2.

Écrite comme tu l'as fait, ta dernière ligne du message #9 est fausse, il n'y a pas égalité. En rajoutant les oubliés (développement limité), on peut le rendre correct.
Par ailleurs, je n'ai pas compris pourquoi tu parles de limites.

Cordialement.

[gts2]

Écrite comme tu l'as fait, ta dernière ligne du message #9 est fausse, il n'y a pas égalité. En rajoutant les oubliés (développement limité), on peut le rendre correct.

Oui, tout à fait, j'ai pris quelques raccourcis ...

Par ailleurs, je n'ai pas compris pourquoi tu parles de limites.

Idem...

Désolé pour les approximations.

[Lzfix]

Merci pour ces explications. J'ai oublié beaucoup de notions depuis mes études ahah.

Pour répondre

donc je ne sais trop par quel bout le prendre.

:
Je ne fais plus vraiment de "math" mais j'apprécie me poser des petits problèmes (de géométrie généralement). Une fois que j'ai trouvé une solution je regarde sur internet voir si j'ai juste ou non puis quand je peux, je calcul sous excel pour voir ce que ça donne sur un graphe (j'aime aussi simplement l'esthétique des courbes formées par certaines fonctions) que je peux manipuler. En utilisant les outils de régression j'observe souvent des approximations. Il suffit de transformer les valeurs des coefficients en nombre plus "logique". Pour exemple n/(tan(π/n)) donne un graphe similaire à un polynome de degré 2 (entre 2 et l'infini) avec pour coefficients a = 0.318 b = 0 et c = -1.047. De la il est assez simple de voir que a = 1/π et c = π/3. Donc j'obtiens que n/tan(π/n) ≈ n²/π - π/3. J'essaie alors avec les maths que je connais et que je peux trouver en ligne de remonter à cette égalité pour voir si elle tiens la route ou non. Ici j'étais bloqué sur les séries de taylor que je connais mais que je ne sais pas vraiment utiliser, et puis j'ai un peu oublié les astuces de changement de variable, d'égalité quand y a des limites...

Je viens de tout récrire, et je retrouve votre résultat donc je suis content merci !