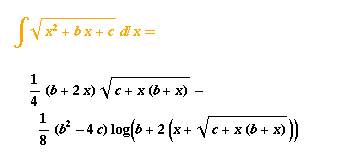Bonjour,
je souhaiterais integrer f(x)
f(x)=( ax^2 + bx + c )^0.5
avec a,b,c des réelles
Dans tout ce que je connai, je n'arrive pas a trouver la solution. C'est ce foutu ^0.5 qui bloque tout. et en plus, a,b,c sont des parametre variant.
PS: cette question découle de la suite des calcule de http://forums.futura-sciences.com/thread126662.html.
En esperant qu'il y est une solution, je vous souhaite une agréable journée.
bon alors d'après moi (je dis bien d'après moi). Le ^0.5 équivaut à ^1/2 qui s'intègre en ^3/2, et le tout divisé bien entendu par 3/2.
Ce que tu dis Trainskill n'est pas tout à fait correct.
Si on avait (2ax+b)( ax^2 + bx + c )^0.5 alors la primitive serait ce que tu annonces : 2/3 * ( ax^2 + bx + c )^3/2.
Mais sans ce terme devant, je ne sais pas comment intégrer ce truc.
Merci pour ta reponse.
Effectivement, ^0.5 correspond a ^1/2 ou encore la racine carré.
Pour calculer mes primitive, je me base sur http://fr.wikipedia.org/wiki/Primiti...%C3%A9matiques)
D'apres le wikipedia je pense que ton résonement est erroné, car tu oublie u'(x)
f(x)=u(x)^n a pour dérivé :
f'(x)=u'(x)*n*u(x)^(n-1)
Donc si je dérive la primitive que tu m'a indiqué, je ne retombe pas sur ma fonction de départ.
Envoyé par CR_Gio
Bien vu, c'est ce que je disais dans mon message d'avant.
Pour avoir une idée de ta primitive, tu peux essayer maple, ou même integrator, le site préféré de ericcc (http://integrals.wolfram.com/index.jsp)
Je savais que je regretterais d'avoir posté cette proposition. Mais j'aurais essayé
GuYem Aujourd'hui 13h19
CR_Gio Aujourd'hui 13h21
La prchaine foi je tacherai d'etre plus rapide ...
Merci de l'info. Je ne connaissait pas. Maleureusement cela ne me serra d'aucune utilité
Mais j'ai continué a creuser et j'ai eu une idée.
Je peut simplifier ma fonction (ax²+bx+c) en posant des condition a ma courbe de bezier. ainssi, j'arrive a :
f(x)=c^0.5 au lieu de (ax²+bx+c)^0.5 meme si je trouve ca bizard(trop simple), je vais aller dans cette direction ...
Merci encore pour l'interet que vous porter a mon post.
Bonjour,
ça "sent" fort le besoin d'un changement de variable pour lequel
onc mettre ax²+bx+c sous forme canonique a(X²+e) avec e=+/- 1, X étant de la forme dx+f, puis changement X=cos(u) (ou sin(u)) si e=-1, X=ch(u) ou sh(u) si e=+1.
C'est pénible mais ça aboutit.
Cordialement
[Grillé par Homotopie !]
Tu dois intégrer une expression de la forme
Je suppose que ton a est non nul, donc cela revient, en divisant tout par a, à intégrer
En posant u=x+b/2, donc dx=du, on se ramène à
Ensuite, soit tu fais le changement de variable recommandé par Homotopie, soit tu connais ce genre de primitive par coeur, soit tu vas sur The Integrator
Merci
Pouvez vous neanmoins me confirmer le résultat ?
a pour intégrale :
=\frac{(2x+a+b)\sqr{x(x+a+b)}}{4}-\frac{(a+b)^2\ln(2\sqr{x(x+a+b)}+2x+a+b)}{8})
Merci pour toute l'aide que vous m'avez apporté.
PS: j'étais sur le point de laisser tombé, me consolant en me disant que c'était imposible
Me revoila encore.
Je n'arrive vraiment pas a integrer cette fonction. j'ai télechargé maple (un organiseurj'ai pas du trouvé le bon logiciel ...), integrator un logiciel de graphisme ...
J'ai du mal a comprendre la demarche a suivre pour réaliser le changement de variable.
Me voila plus a terre maintenant en vous demande s'il vous plai de me donner la primitive de (x^2+bx+c)^0.5
La primitive, tu viens de l'écrire plus haut !
Oui je déséspere ....
Bon ok j'ai trouvé integrator il me donne :
Le résultat que j'ai donné audessus vien de ma calculette.
Mais je ne trouve jamais la meme chose avec deux systeme de calcule different. C'est pourquoi je vous demande votre résultat.
Dérive les primitives et retrouve le résultat.
