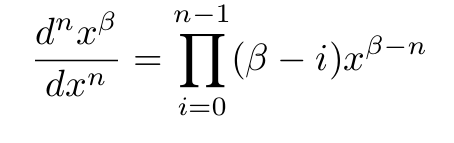Dérivée k-ième de x^{n}

Bleyblue · 11/08/2005 - 21h54

Bonjour,

J'essaie de trouver une expression de la k-ième dérivée de $f(x) = x^{n}$

f' = $nx^{n-1}$
f'' = $n(n-1)x^{n - 2}$
f''' = $n(n-1)(n-2)x^{n-3}$

Donc moi je dirais :

$\frac{d^n}{dx^n} (x^k} = \frac{k!}{(k - n)!} . x^{n - k}$
mais cette formule n'est valide que pour k naturel. De plus il faut supposer k > n ce qui n'est pas forcment le cas.

Vous auriez une formule plus générale à proposer

?

merci

LocalStone · 11/08/2005 - 22h18

Je suis pas mathématicien, loin de là, mais j'ai peut-être une idée ...
On peut pas dire que $\forall (x, n) \in R^{+}_{*} \times R, x^{n} = e^{i \ln(x)$ ?
Où en tout cas jouer sur le fait que les puissance ne soient en fait qu'une association de logarithme et d'exponentiel ...
Si ça peut aider ...
++ !

LocalStone · 11/08/2005 - 22h37

J'ai fait des calculs

, et en fait, la formule pour la dérivée est aussi bien valable pour k entier que pour k réel ... Je savais pas non plus ...

Bleyblue · 12/08/2005 - 18h02

Ma formule à moi n'est valable que pour k naturel étant donné que x! n'est définit que pour x naturel.

Sinon avec ta méthode cela pourrait aller mais je pense que je suis sensé y pavenire sans celle ci (c'est un exercice qui vient de mon livre d'analyse et à cette partie la le lecteur n'est pas sensé connaître les dérivées de fonctions logarithmiques ...)

merci

phenomene · 12/08/2005 - 18h11

Bonjour, les formules sur les factorielles peuvent se prolonger grâce à la fonction Gamma d'Euler. C'est une fonction définie pour tout nombre complexe de partie réelle strictement positive, et en particulier pour tout réel strictement positif donc. Elle vérifie la propriété $\Gamma(n+1)=n!$ pour un entier naturel $n$ , et la même relation fondamentale que la factorielle : $\Gamma(z+1)=z\Gamma(z)$ .

Mais le plus simple est probablement de laisser tes $n(n-1)(n-2)\ldots(n-k+1)$ tels quels sans chercher à les remplacer par des factorielles, ainsi ta formule reste valable pour $n$ réel sans problème.

Au fait, il me semble que tu intervertis des $k$ et des $n$ dans ta formule.

Florette · 12/08/2005 - 18h26

Bonjour,
Mathematiquement on peut derviver n fois une fonction avec n non naturel? C'est ce que vous aves l'air de dire alors je demande!
Merci

chrisgir · 12/08/2005 - 18h35

Non on ne peut pas dériver un nombre réel de fois une fonction. n doit être naturel.

phenomene · 12/08/2005 - 19h11

Envoyé par Florette

Bonjour,
Mathematiquement on peut derviver n fois une fonction avec n non naturel? C'est ce que vous aves l'air de dire alors je demande!
Merci

On peut en effet étendre le concept de dérivation à un ordre non entier, mais c'est assez compliqué (cela fait appel à la théorie des distributions, ou à celle de la transformée de Fourier, par exemple).
Un copain a fait une thèse d'histoire des maths là-dessus et en parle un peu sur une page web qui a l'air accessible au non-spécialiste : http://s.dugowson.free.fr/recherche/dones/DONE.html.

Mais dans ce fil, rien de tout ça, il y a juste eu interversion de $n$ et $k$ par l'intervenant initial ! Bref, c'est une erreur...

Bleyblue · 13/08/2005 - 17h46

Mais le plus simple est probablement de laisser tes $n(n-1)(n-2)\ldots(n-k+1)$ tels quels sans chercher à les remplacer par des factorielles, ainsi ta formule reste valable pour $n$ réel sans problème.

Au fait, il me semble que tu intervertis des $k$ et des $n$ dans ta formule.

Ahh ben oui ... je n'avais pas pensé à (n - k + 1) tiens.
Sinon oui en effet j'ai interverti n et k par erreur dans ma formule.

Donc en fait :

$\frac{d^nx}{dx^n}(x^{k}) = n(n-1)(n-2) ... (n - k + 1)x^{k - n}$

merci

Zuriv · 13/08/2005 - 18h20

k(k-1)...(k-n+1) . x^(k-n) plutot, si tu dérive x^k

phenomene · 13/08/2005 - 18h22

Allez, mon dernier mot sera :
$\frac{d^k}{dx^k}(x^n)=n(n-1)\ldots (n-k+1)x^{n-k}$ .

Bleyblue · 13/08/2005 - 19h31

Décidément, je fais des fautes partout

Un grand merci !

LocalStone · 13/08/2005 - 22h38

Et bah je viens d'apprendre que l'on peut faire une dérivée d'ordre 1,5 ... Euh ... Compliqué ... J'ai du mal à admettre ...

Bleyblue · 14/08/2005 - 18h48

Hé

?

C'est bizarre ça, dérivé 1,5 fois une fonction

LocalStone · 14/08/2005 - 23h54

Je suis bien d'accord

... Mais lui, http://s.dugowson.free.fr/recherche/dones/DONE.html, il dit que si !

Dérivée k-ième de x^{n}

Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Re : Dérivée k-ième de x^{n}

Discussions similaires

dérivée n ieme

dérivée n-ieme

conjecture de la n-ième dérivée de 1/x et démonstration par récurrence

derivee n-ieme d'une fonction composee

dérivée n-iéme de (1+x²)^(n-1)

Les tags pour cette discussion