Distribution uniforme de points sur sphère.

[281281]

Bonjour,

N'étant absolument pas issu d'une formation scientifique, je coince aujourd'hui sur un problème de géométrie. C'est un problème de 3D.

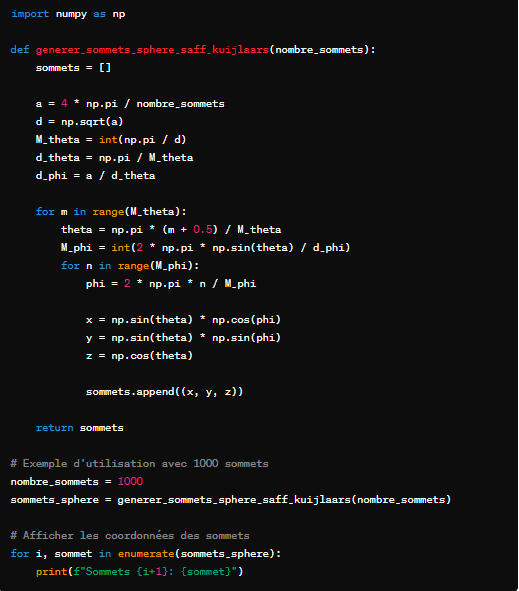
Je cherche à distribuer un nombre entier N de points à la surface d'une sphère (en d'autres termes, tous à la même distance R, le rayon, d'un centre C situé à 0, 0, 0.) qui soient tous équidistants de proche en proche. Je cherche une méthode ou une formule qui me permette de construire cette sphère avec un N quelconque (Le minimum serait N=4 et cela donnerait un tétraèdre).
Les polyèdres réguliers remplissent les conditions recherchées je crois; par exemple, le cube pour N=8, ou l'icosaèdre pour N=12, ont leurs sommets inscrits sur une sphère, etc... Mais je cherche une solution, au moins approchée, pour tout N entier existant.

Une solution approchée pourrait être de trouver la formule qui me permet de construire et disposer tous les sommets d'une sphère géodésique (Je veux dire, comme les dômes géodésiques) simplement avec N comme seule information de départ.

Merci infiniment à tous ceux qui aurait une petite idée ou des liens à me proposer. Il s'agit d'un projet de diplôme.

Christophe.

[Jeanpaul]

Cette distribution de points va générer un polyèdre régulier inscrit. Tous les nombres N ne sont pas possibles, c'est connu depuis les Grecs et encore mieux depuis Euler.
Voir le site :
http://chronomath.com/
et taper "polyèdre"

[281281]

Merci beaucoup.

Quelqu'un connaîtrait-il une solution approchée, tout du moins visuellement, et simple à calculer ?
J'entends par là, par exemple, la construction d'une sphère géodésique à partir seulement du nombre N de sommets.

Christophe.

[Le_boulet]

Salut,

Il y a, sur ce sujet, un article dans le numéro de juillet 2005 de "Science et vie"

Bon ! comme d'hab, ils ne vont pas loin dans le formalisme mathématique (vulgarisation oblige), mais ça te donnera sûrement des pistes et des idées.

Le principe est de simuler le comportement de charges qui se repoussent sur la surface d'une sphère, jusqu'à un état d'equilibre.

[gillesh38]

Pour appuyer ce que dit Jean Paul, il n' y a QUE les 5 polyèdres réguliers (platoniciens ) qui répondent à ton problème N = 4 (tétraèdre), 6 (octaèdre), 8 (cube), 12 (dodécaèdre), 20 (icosaèdre). Pour N différent de ces valeurs, il y a une solution "optimale" mais pas régulière.

[martini_bird]

Salut,

une petite question: les sommets des solides de Poinsot sur la sphère circonscrite correpondent aux sommets d'un solide de Platon?

Merci d'avance.

[saroule]

Bonjour,

Une méthode de calcul existe pour une répartition équilibrée de N points sur une sphère. Elle a été développée par 'saff et kuijlaars'.
En transcrivant les équations sur 'Excel' on obtient facilement les coordonnées sphériques ou cartésiennes des N points. Le graphique correspondant permet ensuite de visualiser cette répartition sur la sphère.

[Ksilver]

Pour appuyer ce que dit Jean Paul, il n' y a QUE les 5 polyèdres réguliers (platoniciens ) qui répondent à ton problème N = 4 (tétraèdre), 6 (octaèdre), 8 (cube), 12 (dodécaèdre), 20 (icosaèdre). Pour N différent de ces valeurs, il y a une solution "optimale" mais pas régulière.

Non il y en a plu que 5 avec les condition qu'impose 281281. les polyhédres ayant plusieur type de faces sont aussi admisible (le 'balon de foot' par exemple, mais il y en a des plus simple)

Ceci dit ca fait toujours un nombre finit de polyhèdres - je ne me rapelle plus combien exactement, mais beaucoup plus que 5.

sinon le probleme de répartir régulièrement n point sur une sphère n'est pas encore résolue. pour chaque définition de "régulierement" on arrive à des solution aproximative, mais aucune n'as encore donné de solution exacte pour tous n. avec la tienne, il n'y aura probablement pas de solution. mais on peut ce demander :
-comment répartir n point sur un surface de facon à maximiser le minimum de distance entre deux point.
- comment ce répartirai n billes chargés identiques (qui ce repousse selon les lois de l'électrostatique...)

[breukin]

qui soient tous équidistants de proche en proche

Cette propriété mérite d'être définie !
Car normalement, "de proche en proche" signifie que, à partir d'un point donné, on classe de proche en proche les autres points en fonction de la distance (soit le plus petit arc sur la sphère, soit la ligne droite dans l'espace).
On obtient donc des sous-ensembles de points, dont la propriété, au sein de chaque sous-ensemble, est d'être équidistants (ces sous-ensembles pouvant cependant comporter un seul point).
Donc toute distribution finie de points vérifie la propriété que tous les points sont équidistants, "de proche en proche" !
Donc sans aucun doute, cette expression est mal appropriée ?

[Badger]

Bonjour à toutes et à tous

Est-ce possible d'avoir accès à des coordonnées sphériques ou cartésiennes d'une répartition de 16 points (même approchée) sur une sphère pour que chaque point soit au centre d'une surface de la sphère et que toutes les surfaces soient de la même dimension ?

En vous remerciant

A bientôt