Bonjour,
je suis un lycéen et je travail sur un problème.
Suite à quelques recherches j'en suis venu à rechercher le vecteur propre d'une matrice 3*3 si quelqu'un peut m'aider... J'aimerais la formule générale et détaillée. (je ne suis qu'au lycée)
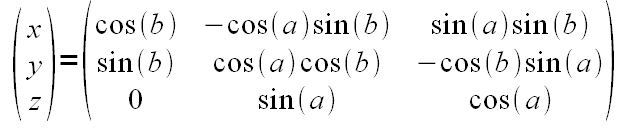
les vecteurs propres d'une matrice 3*3 sont détermine avec la formule suivante :
Apres tu calcule le determinant de A
et tu va trouver une équation avec lecomme inconnu.
tu résout l'équation
Voila pour le debut
Ok merci,
en fait je travail sur les rotations d'une sphère au cours de multiples lancés, donc la matrice que j'utilise à des angles variables... cela pose un problème dans la formule?
De plus j'utilise deux angles pour arriver à caractériser la rotation totale de la sphère (un pour la longitude, un autre pour la latitude)
Pour plus de clarté je vous fournis ma matrice:
La matrice
Tu transposes la matrice :
Tu calcules la différence de ces matrices qui est de la forme :
Un vecteur propre de
Bonjour,
Tout d'abord, que signifie (x, y, z) = une matrice ? D'où vient cette formule ?
Pour ce qui est des vecteurs propres, ta matrice est un cas assez particulier car il s'agit d'une matrice de rotation, qui possède pas mal de propriétés intéressantes, je t'en fait une liste rapide :
- sa transposée est égale à son inverse
- son déterminant est égal à 1
- ses valeurs propres sont de module 1
- ici si ta rotation n'est pas une rotation d'angle pi, une de ses valeurs propre est 1
Il te reste en fait plusieurs moyens après pour calculer ses valeurs propres. Soit tu reviens à la définition : tu calcules le déterminant de (M-XI3) qui sera un polynôme de degré 3 et les racines te donneront les valeurs propres, comme l'a dit indilunique.
Soit tu utilises les différentes propriétés des valeurs propres, par exemple le fait que leur produit donne le déterminant de la matrice, que leur somme donne la somme des termes diagonaux de la matrice, ce qui peut simplifier tes calculs.
Mais comme tu es au lycée, peut-être ne veux-tu pas partir dans ce genre de considérations et juste appliquer la définition, à toi de voir.
Silk
PS : si tu reviens à la définition et calcules le polynôme, tu devrais vérifier que 1 en est racine et le factoriser par (X-1) pour te ramener à une équation du second degré.
Désolé pour le double-post mais je viens de me rendre compte qu'il cherchait le vecteur propre de la matrice et pas ses valeurs propres donc ma réponse précédente est totalement inutile et risque de plus embrouiller qu'autre chose, mais je ne peux plus éditer. Si un modérateur passe par ici et peut supprimer mes messages, ça serait bien.
