Bonjour à tous,
Je suis en train d'étudier une définition de la fonction de Dirac. Seulement voilà, je suis obligé de permuter une limite et une intégrale lors d'une étape et ça me gène de le faire sans rien justifier.
Ma question est alors quel théorème utilisé? Sachant que la limite à l'intérieur de l'intégrale (dont la variable est w) est la suivante:
Je ne peux pas utiliser le théorème de convergence monotone puisque ce n'est pas une suite de fonction fn avec n tendant vers l'infini.
Quel théorème dois-je donc utiliser?
Merci pour vos réponses.
-----




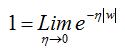

 ), utilises le théorème de convergence monotone pour obtenir la convergence le long de cette suite, puis utilise un encadrement pour les valeurs de
), utilises le théorème de convergence monotone pour obtenir la convergence le long de cette suite, puis utilise un encadrement pour les valeurs de