Bonjour à tous,
Je n'arrive pas à résoudre une équation complexe d'électricité, et j'aimerai vivement connaitre la méthode :
A savoir : mettre sous la forme : z=(a+jb)/(c+jd) : de cette équation :
Le but étant de tout mettre au même dénominateur et simplifier afin de donner l'expression des réel (a et c) et imaginaire (c et d) sous la forme d'un polynôme en oméga !
Merci à tous !
-----




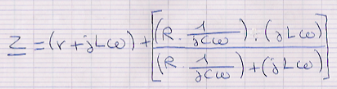
 et
et 





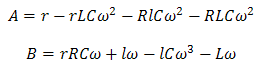
 ça m'a permis de beaucoup mieux comprendre le DVP.
ça m'a permis de beaucoup mieux comprendre le DVP.