Suite semi-arithmétique

[Aenonis]

Bonjour à tous et à toutes,

Je sèche sur un problème mathématique que je me suis fixé pour régler mes soucis financiers.

Étant une forte tête en maths, je m'étonne de ne pas trouver de solution.

En fait, j'ai trouvé une solution que j'ai calculé à la main et je voulais informatiser le calcul avec un logiciel permettant de faire du calcul formel (j'utilise Maple 12) afin de pousser plus loin les démarches.

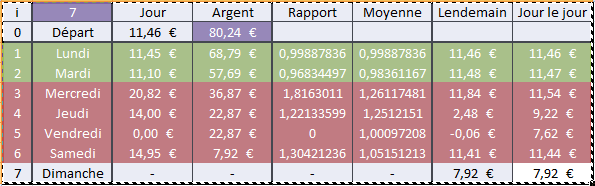
Je vous présente le modèle mathématique que j'ai réalisé pour modéliser mes finances.

En effet, ce modèle s'agence autour d'une suite "semi-arithmétique", je m'explique: la suite fonctionne comme une suite arithmétique mais à la seule différence près que la raison de la suite est variable, ce qui complique fortement la modélisation sur Maple.

Voici l'équation de départ: avec .
correspond à l'argent hebdomadaire que je reçois chaque semaine.
L'index correspond au numéro du jour dans la semaine.
Les variables correspondent à l'argent dépensé le jour .
La suite correspond à l'argent qui me reste à la fin du jour .
De cette équation, on peut tirer une formule intermédiaire qui va nous servir pour la suite: .
Je calcule le rapport quotidien qu'il y a entre l'argent dépensé et l'argent que j'ai reçu: ainsi (, c'est le nombre de jours dans la semaine, pouvant être adapté selon les besoins) que la moyenne des rapports (le rapport hebdomadaire): qui, grâce à la formule intermédiaire, peut se simplifier en .

Voilà le modèle.

De là, j'ai essayé, avec succès, de trouver des formules qui permettent de revenir sur le droit chemin si j'ai été trop dépensier en début de semaine.

La formule qui permet de se redresser dès le lendemain s'obtient avec le prédicat suivant: , en effet, le modèle est équilibré lorsque le rapport hebdomadaire est égal à l'unité.
De fait, en utilisant les équations du modèle, on obtient l'équation tant convoitée:

Vu que cette formule peut amener des nombres négatifs, j'ai pensé à différentes formules qui tendraient vers l'équilibre du modèle au jour le jour, pour ne pas corriger les excès dès le lendemain, mais sur le restant de la semaine.
De ce fait, j'ai retiré une formule simple: , qui divise simplement la somme restante par le nombre de jours afin de partager équitablement l'argent qui me reste.

J'ai essayé, sans succès cette fois-ci, d'introduire le modèle sur Maple et d'exécuter les différents "rsolve" pour retomber sur les deux formules de redressement.

Pourquoi voudrais-je que ça fonctionne sur Maple? En effet, au début de cet article, je voulais approfondir les différents types de redressement que je peux avoir.

Si je veux un redressement particulier, par exemple: une punition lors d'excès trop élevés, on peut utiliser la fonction (ou tout autre fonction, j'aimerai que le modèle soit modulaire) afin de limiter les dépenses les premiers jours (au début monte doucement) puis de permettre des dépenses plus élevées ( monte comme une flêche par après), toujours en tenant compte de l'argent réel dépensé.

En gros, un "docteur" financier pour m'aider.

Avec Maple, je m’emmêle les pinceaux, vu qu'on cherche une valeur particulière de en fixant une autre variable ( ou ), dans la récurrence, il foire complètement vu que les données sont les ...
Et je ne sais pas du tout comment je peux faire pour arranger le bazar.
De plus, je ne sais pas comment modéliser (mathématiquement) le redressement particulier que j'ai énoncé ci-dessus.

En vous remerciant d'avance,

Aenonis

[Aenonis]

Petit oubli de ma part:

On remarquera que la raison de la suite est variable (c'est ça toute la complexité du modèle), en effet, on a et non pas (constant).

[taladris]

Salut,

En effet, ce modèle s'agence autour d'une suite "semi-arithmétique", je m'explique: la suite fonctionne comme une suite arithmétique mais à la seule différence près que la raison de la suite est variable, ce qui complique fortement la modélisation sur Maple.

Voici l'équation de départ: avec .

tout suite peut s'écrire sous cette forme: il suffit de poser . Si tu imposes aux d'être tous (strictement) positifs, alors toute suite (strictement) décroissante peut être mise sous cette forme. C'est pour cela que Maple ne peut pas résoudre l'équation. Il y a trop de solution et aucune formule générale pour les décrire. Si les ont une forme spéciale, tu pourrais peut-être obtenir quelque chose.

Je calcule le rapport quotidien qu'il y a entre l'argent dépensé et l'argent que j'ai reçu: ainsi (, c'est le nombre de jours dans la semaine, pouvant être adapté selon les besoins)

Je ne comprends pas. le rapport quotidien qu'il y a entre l'argent dépensé et l'argent que j'ai reçu est seulement , non? Pourquoi multiplier par n?



Pour finir, un avis personnel: je ne comprend pas l'intérêt de la démarche. Si tu ne connais pas (au moins de manière approximative) à l'avance, la valeur des , tu te retrouves le i-ème jour avec une certaine somme d'argent, et il tu "suffit" de ne pas dépenser ce qui te reste. Et si tu connais les à l'avance, pourquoi ne pas faire un budget en début de semaine et vérifier que les dépenses collent avec tes recettes?

Si jamais tu veux simuler le caractère aléatoire de tes dépenses, ton formalisme n'est pas suffisant. Il faut te tourner vers les probabilités et les statistiques.

Cordialement

PS: malgré le caractère sceptique de ma remarque finale, je trouve que c'est tout à ton honneur de se chercher des problèmes et de tenter de les résoudre.

[Aenonis]

Bonjour,

Je te remercie pour cette réponse rapide.

Je suis d'accord pour qu'elle soit décroissante (et non strictement) vu que . Mais je ne vois pas le rapport avec le caractère infini de cette suite vu que les sont connus à l'avance. De fait, je réponds à ta troisième interrogation: en connaissant les de à , on cherche une valeur de selon certaines conditions (j'en ai présentées deux).
Concernant ta deuxième interrogation, il est vrai que le rapport quotidien est de mais pour des raisons de facilité, je normalise le résultat en multipliant par afin de voir directement si le système est à l'équilibre ou pas: en-dessous de 1, on est en positif, au-dessus de 1, on est en négatif. Je ne sais pas si cette normalisation a un effet néfaste.

Bien à vous,

Aenonis

[taladris]

OK pour la multiplication par n dans le rapport. Et effectivement, même si tu ne l'avais pas précisé, il est logique de supposer pour tout i.

Cependant, je ne comprend toujours pas ce que tu souhaites faire. Peux-tu donner un exemple numérique?

[Aenonis]

Voilà l'exemple numérique:
exemple.png

Bien à toi,

Aenonis

[taladris]

Salut,

merci pour l'exemple. Cependant, je ne le comprend pas ^^.

Quelles les données connues? Et quel est le résultat que Maple est sensé renvoyer?

[Aenonis]

Les données connues sont "Jour", "Argent" et les deux données violettes.
Maple est censé renvoyer "Lendemain" et "Jour le jour" mais ça ne va pas vu que Lendemain et Jour le jour sont les x(i) calculés alors que les x(i) sont les données connues également, donc Maple m'envoye gentiment sur les roses.

Merci,

Aenonis

[Aenonis]

Tu as vu ?

[taladris]

Salut,

désolé, je voyageais un peu ces derniers temps. Et je ne suis pas sûr d'avoir compris ce que tu veux.

Laisse-moi résumer ce que je comprends: tu disposes d'une suite de réels strictement positifs. Tu fixes un réel strictement positif et tu définis par l'équation

(*)

En fait, tu ne connais que les premières valeurs de (disons jusqu'à ) et tu voudrais calculer les autres en résolvant (*), c'est ça? Ou plus précisément, tu voudrais que Maple détermine les valeurs de de sorte que soit positif?

Cordialement

[Aenonis]

Bonjour,

Il y a une petite erreur dans ta compréhension: en effet, la suite commence à .

En effet, je connais les jusqu'à et je souhaite que mapple calcule avec comme première formule simple: .

Cela peut paraître simple en soi mais je suis perdu.

Merci.

Aenonis

[Aenonis]

Maintenant que je réfléchis, tu as entièrement raison, j'aimerai que Maple calcule les pour que ou soit positif. En effet, Maple ne sait rien faire avec ce modèle, il faut donc ajouter une "suite logique" aux tels que avec une fonction quelconque.

Tu m'as donné la solution mathématique et j'ai pu modéliser sur ta compréhension.

Reste plus qu'à résoudre ça mathématiquement et informatiquement (avec Maple).

En te remerciant,

Aenonis