Géométrie et fonction

[invite6ebdfb3e]

Bonjour, j'ai besoin d'aide cqar j'ai un dm à rendre pour mardi et je suis bloqué sur une question ...

Enoncé:

Dans cette exercice, les longueurs sont exprimées en cm, les aires en cm², et les volumes en cm3.
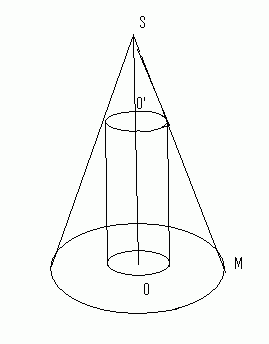
Le cône représenté ci-contre a pour rayon OM =6 et pour hauteur SO = 12.
On coupe ce cône par un plan parallèle à la base comme indiqué sur la figure de telle manière que SO' = x.
On construit alors le cylindre qui a le même axe que le cône pour rayon [O'M'].



1. Dessiner en vrai grandeur le triangle SOM et placer O'M'

J'ai donc placé O' n'importe ou sur la figure car c'est en fonction de x et j'ai tracé une droite perpendiculaire à OO' pour trouvé M'


2.Démontrer que O'M' = 0,5x

J'ai écrit: Dans le triangle SOM on sait que 0' appartient à SO et M' appartient à SM et que O'M' // OM
Donc d'après le théorème de Thalès on a SO'/SO = SM'/SM = O'M'/OM
<=> x/12 = 0'M'/6
<=> O'M' = 6x/12
donc 0'M' = 0,5x
3. Exprimer OO' en fonction de x.

Là j'ai écrit f(x) = 12-x mais je sais pas si c'est plus juste d'écrire 00'= 12-x

4.Démontrer que le volume V(x) du cylindre peut s'écrire: π (3x²-0,25x^3)

Je suis bloqué à la question là... J'ai trouvé que pour calculer l'aire du cylindre on fais : πR²H mais ensuite je n'arrive pas à établir de lien entre cette formule et l'équation à démontrer..

Merci de m'aider dans mon raisonnement ce serait très gentil ...

Coordialement
Pauline.
-----

[phys4]

3. Exprimer OO' en fonction de x.

Là j'ai écrit f(x) = 12-x mais je sais pas si c'est plus juste d'écrire 00'= 12-x

Il est inutile de créer une fonction f(x), l'écriture OO' = 12 - x est suffisante.

4.Démontrer que le volume V(x) du cylindre peut s'écrire: π (3x²-0,25x^3)

Je suis bloqué à la question là... J'ai trouvé que pour calculer l'aire du cylindre on fais : πR²H mais ensuite je n'arrive pas à établir de lien entre cette formule et l'équation à démontrer..

Vous avez l'expression correcte du volume et vous connaissez sa hauteur H = OO' ainsi que son rayon O'M', il suffit de remplacer.

Bonne suite.