J'ai procédé de cette façon : 3r²-r+10 = cos(nPi/4) + 1/(n+1) et resolu le polynôme du 2eme degret enfin je l'ai factorisé
Puis j'ai eu ceci
3( S(indice n+1) - 2 ) (S(indice n+1) - 5/3 ) = cos(nPi/4) + 1/(n+1)
Je Suis bloquée .. Suis-je dans le bon chemin ou pas ?
c'est la seule idée qui m'est venue en tete
-----




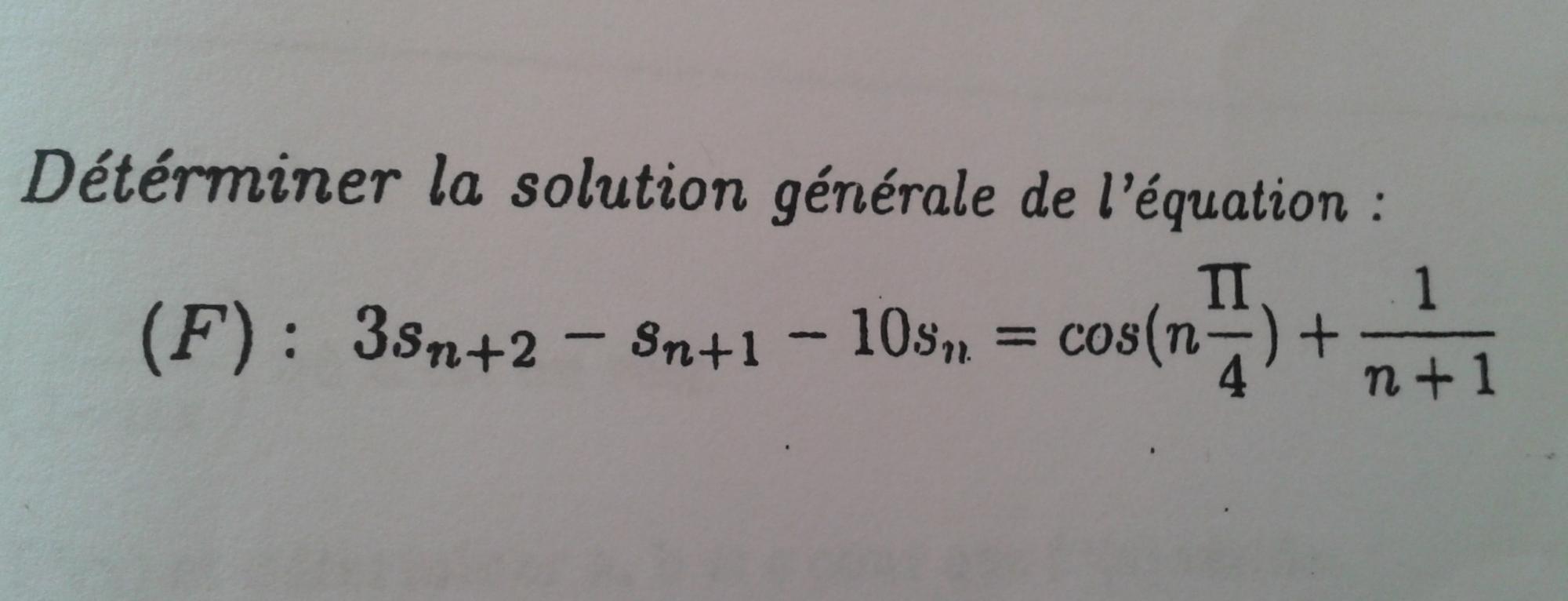


 (en utilisant l'équation caractéristique bien sûr).
(en utilisant l'équation caractéristique bien sûr).