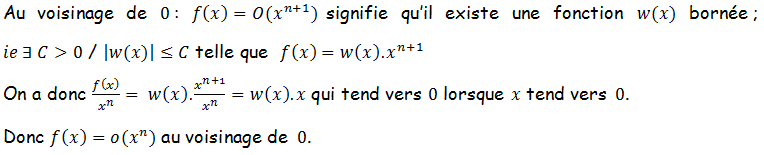Bonjour,
Je travaille sur les développements limités de fonctions, et en me promenant à droite à gauche je trouve des o ou O.
Par exemple pour e^x:
petit o.PNG
ou
grand O.PNG
Alors je sais que o implique O, et jusque là tout va bien.
Mais doit-on en déduire de ces deux développements que o(x^n) implique O(x^n+1)? Ou est-ce que cela n'a rien à voir?
En lisant des cours je trouve comme condition à l'utilisation de la formule de Taylor le fait que la fonction soit n fois dérivable et on utilise o, le fait qu'elle soit n+1 fois dérivable et on utilise O, et à nouveau se pose la question du lien entre o(x^n) et O(x^n+1).
Bref tout ceci m'a embrouillé, et j'aimerais comprendre, parce que je ne trouve pas de solution, si on peut conclure à un lien entre o(x^n) et O(x^n+1)?
Merci d'avance.
-----





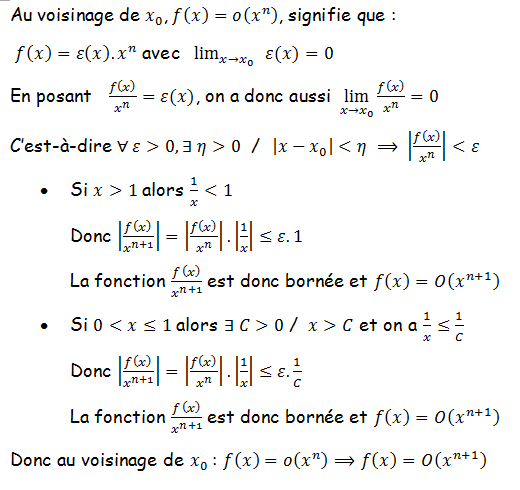
 alors il existe
alors il existe