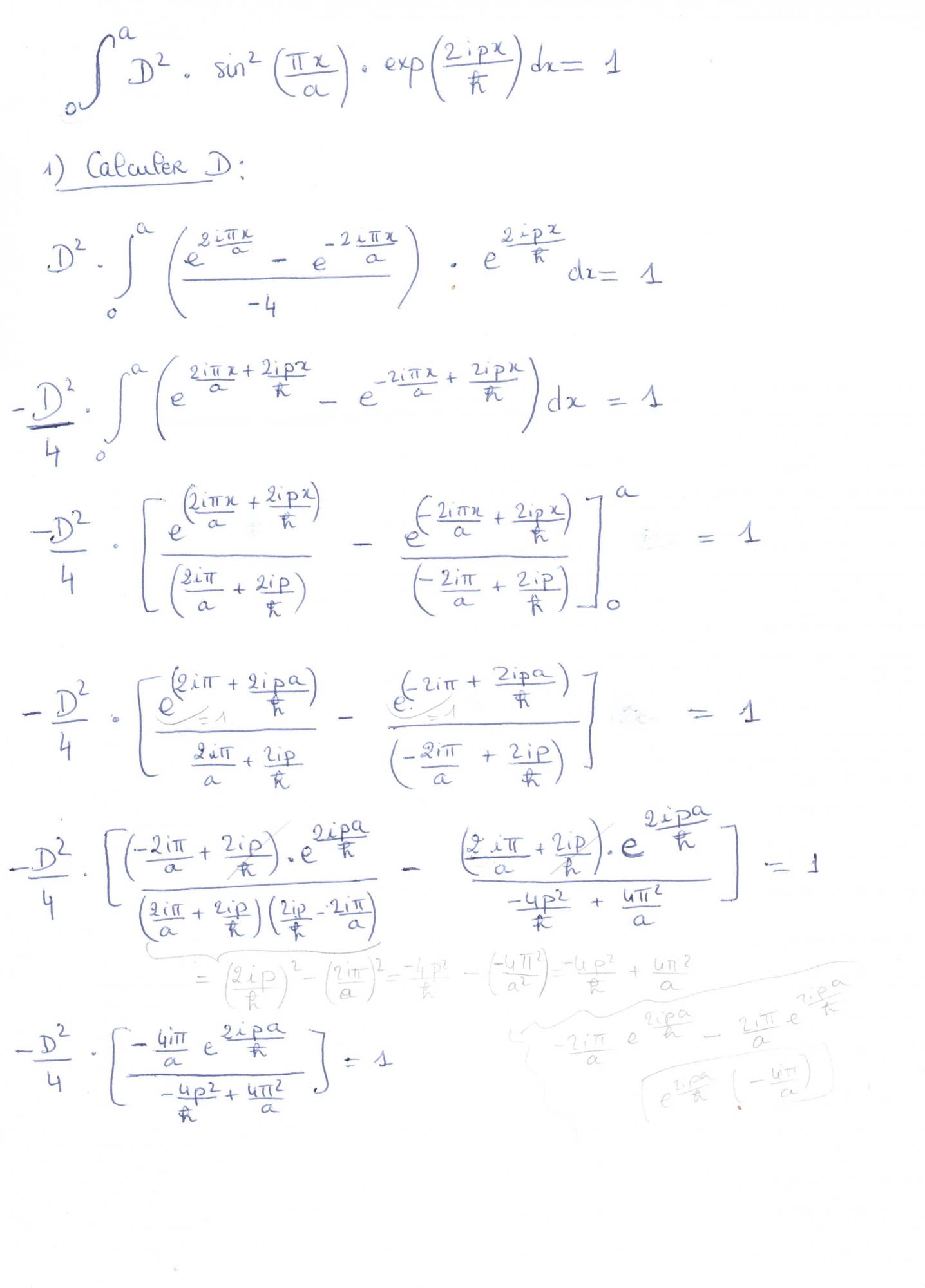Calcul qui n'aboutit pas...
Discussions similaires
-
Par Myr dans le forum Mathématiques du collège et du lycée
Réponses: 1
Dernier message: 07/03/2012, 20h53
-
Par cedbont dans le forum Physique
Réponses: 3
Dernier message: 11/10/2008, 20h42
-
Par invite234d9cdb dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 18/10/2006, 09h32
-
Par invitef50c1f06 dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 21/02/2006, 18h31