Bonjour à tous,
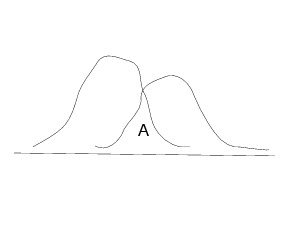
Je cherche à calculer l'aire (A) sous l'intersection de 2 lois normales (de densité f1 et f2, moyennes et ecart type µ1, o1, µ2, o2).
Pour moi cela s'écrit de cette facon:
Ce qui donne donc l'expression suivante:
Et la j'ai du mal sur l'intégration, j'ai essayé de développer les différents termes, mais je ne tombe sur rien qui me soit vraiment utile...
Quelqu'un aurait une idée?
Merci
-----