Nombres pyramidaux 1eS

[invite4b0b4f95]

Bonjour à tous,
Je viens de commencer les suites mais je ne maîtrise pas encore ! donc j'aimerais bien que vous m'aidiez pour ce problème car je me mélange tout entre un et n ! C'est un problème assez guidé mais j'ai du mal avec la suite vous verrez je vous donnerais mes idées à la fin de l'énoncé !

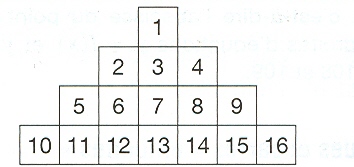
On suppose que la suite des entiers naturels est écrite dans un tableau selon la disposition en pièce jointe.

Objectif : préciser la position de 2001 dans le tableau.

1 Etudions la position de ces nombres pour voir comment il est possible de repérer l'un deux. Les nombres sont écrits en ligne et chaques ligne contient des cases. On peut donc repérer un nombre en disant il est dans la ligne n et dans la p-ième case de celle-ci en partant de la gauche. ( par exemple 14 est dans la 4e ligne et dans la 5e case en partant de 10).
Voyons comment sont disposées les cases par ligne : ligne 1, une case ; ligne 2, 3 cases; ligne 3, cinque cases. Il semble que le nombre de cases par ligne est en progression artihmétique.
Appelons don un le nombre de cases de la n-ième ligne.

Que pouvez vous dire de la suite (un)? Préciser ses éléments caractéristiques.

Mois j'avais pensé à fair n = un-1 + 2
car si je prend des exemple la ligne 1 est égale a
n1 = un0 + 2
n1 = 0+2 quoique non ça marche pas pour le 1 mais pour
n2 = un1 + 2= 1 + 2 = 3
n3 = un2 + 2 = 3 + 2 = 5 ça marche
le problème c'est qu'on me parle de la suite (un) donc je pensais changer les termes de cotés mais ça me donne
un-1 = n - 2
donc un = n + 2 - 2 + 2 = n + 2
et si je prend un ex u2 = 2 + 2 = 4 (car u2 est dans la deuxième ligne)donc ça ne marche !
j'espère que vous comprendrez ce que je vous dit car c'est aussi confus ici que dans ma tête et j'ai vraiment du mal je compte sur vous pour me clarifier cet exercice !
merci d'avance.
-----

[nissart7831]

Voyons comment sont disposées les cases par ligne : ligne 1, une case ; ligne 2, 3 cases; ligne 3, cinque cases. Il semble que le nombre de cases par ligne est en progression artihmétique.
Appelons don un le nombre de cases de la n-ième ligne.

Que pouvez vous dire de la suite (un)? Préciser ses éléments caractéristiques.
.

Bonjour,

utilise ce qu'on te donne dans l'énoncé. Vous êtes guidés, il faut en profiter.
Pour comencer ce problème, il faut savoir de quoi on parle. Alors,

n reprèsente le numéro de la ligne de ta pyramide en partant du sommet et
représente le nombre de cases constituant la ligne numéro n en partant du sommet

On te dit qu'"il semble le nombre de cases par ligne est en progression artihmétique".
Qu'est ce que ça veut dire pour toi? Tu dois avoir remarqué comment progresse le nombre de cases d'une ligne à l'autre de la pyramide. Traduis ça en termes mathématiques avec les définitions qu'on a posé pour n et

[invite4b0b4f95]

Qu'est ce que ça veut dire pour toi? Tu dois avoir remarqué comment progresse le nombre de cases d'une ligne à l'autre de la pyramide. Traduis ça en termes mathématiques avec les définitions qu'on a posé pour n et

J'avais pensé à une suite arithémtique de raison 2 car d'une ligne à la suivante on ajoute toujours deux cases c'est pour ça que j'avais mis + 2 ! mais je n'arrive pas a organiser mes nombres !
= + 2
ça donnerai ça alors ? mais la je n'ai plus n tout seule représentant le numéro de la ligne ?

[martini_bird]

Salut,

le même problème a été posté très récemment.

Cordialement.

[A voir en vidéo sur Futura]

[nissart7831]

Voilà tu as bien compris : tu as 2 cases de plus à chaque ligne et donc tu as bien exprimé cela mathématiquement :



Ton n est toujours là, il est le n contenu dans .
Pour le moment, tu n'as pas encore exprimé directement en fonction de n, mais tu as déjà une relation entre les nombres de cases de deux lignes consécutives.
C'est une suite arithmétique, donc tu sais exprimer le terme général de cette suite, c'est-à-dire, exprimer en fonction de n. Regarde dans ton cours !!

Et donne, comme cela t'est demandé, les caractéristiques de la suite : premier terme, en fonction de n, ...

[invite4b0b4f95]

en fonction de n, mais tu as déjà une relation entre les nombres de cases de deux lignes consécutives.
C'est une suite arithmétique, donc tu sais exprimer le terme général de cette suite, c'est-à-dire, exprimer en fonction de n. Regarde dans ton cours !!

Et donne, comme cela t'est demandé, les caractéristiques de la suite : premier terme, en fonction de n, ...

Dans mon cours j'ai deux relations mais je pencherais plutôt vers la première comme je n'ai pas de ( la première ligne etant ) !
donc ça me ferait = + (n-p) r
mais le truc c'est que dans l'énoncé au debut il me disait que p etait un nombre d'une ligne ! mais la dans ma relation j'ai quoi comme p ? le premier terme serait = 1 , la raison 2
et les caractériqtiques je ne sais pas exactement ce que c'est il faut en dire d'autre ?

[nissart7831]

= + (n-p) r

Cette relation est générale et signifie simplement que tu peux exprimer le terme de ta suite arithmétique en fonction du terme et de la raison r=2 de ta suite arithmétique.
Comme tu dis justement, tu commences à . Donc pourquoi ne pas exprimer en fonction de avec la relation ci-dessus. Qu'est ce que cela donne ?

Pour les caractéristiques, tu peux donner le type de la suite, son premier terme et l'expression de en fonction de n.

[invite4b0b4f95]

Salut,

le même problème a été posté très récemment.

Cordialement.

d'accord mais il a été partiellement traité moi comme formule pour les additions je n'ai pas ça car je ne sais pas à quoi correspondent chaque terme mais en formule générale
S =( n + 1 ) ( + ) / 2
et j'en suis encore à la recherche de mon n

[invite4b0b4f95]

Cette relation est générale et signifie simplement que tu peux exprimer le terme de ta suite arithmétique en fonction du terme et de la raison r=2 de ta suite arithmétique.
Comme tu dis justement, tu commences à . Donc pourquoi ne pas exprimer en fonction de avec la relation ci-dessus. Qu'est ce que cela donne ?

Pour les caractéristiques, tu peux donner le type de la suite, son premier terme et l'expression de en fonction de n.

= + ( n - p ) r
= 1 + 2n -2
= 2n -1
et j'ajoute suite arithmétique

[nissart7831]

= + ( n - p ) r
= 1 + 2n -2
= 2n -1
et j'ajoute suite arithmétique

Oui, suite arithmétique de raison 2, de premier terme 1 et d'expression ...!

Juste une précision de rédaction, dans ta première ligne tu as pris p = 1, donc il faut aussi le remplacer dans (n-p).

[invite4b0b4f95]

Oui, suite arithmétique de raison 2, de premier terme 1 et d'expression ...!

Juste une précision de rédaction, dans ta première ligne tu as pris p = 1, donc il faut aussi le remplacer dans (n-p).

Ok merci ça va beaucoup m'aider pour la fin de l'exercice ! Normalement je devrais m'en sortir mais j'espère pouvoir te retrouver lundi ( car je n'ai pas math avant mardi et j'ai des devoirs à préparer pour avant ) si je ne parvins pas toute seule jusqu'au bout...

[nissart7831]

Ok merci ça va beaucoup m'aider pour la fin de l'exercice ! Normalement je devrais m'en sortir mais j'espère pouvoir te retrouver lundi ( car je n'ai pas math avant mardi et j'ai des devoirs à préparer pour avant ) si je ne parvins pas toute seule jusqu'au bout...

OK, à lundi peut être et bon courage !

[invite4b0b4f95]

Re bonjour,
comme prévu je reviens avec la fin de l'exercice ! je bloque sur une démonstration où je sollicite votre aide.

2- Continuons nos observations. Une ligne contients des nombres consécutifs. Donc pour savoir si un nombre est dans la ligne n, il suffit de savoir s'il est compris entre le premier et le dernier nombre de cette ligne. on note respectivement et , ces nombres.

a) justifiez que = puis que = + 1 ( n supérieur ou egal à 1). Il suffit donc d'étudier la suite ().
Or = 1, =4=+3 car il y a trois cases dans la ligne 2.
b) Prouvez que = + et déduisez en que = +...+.
c) ( c'est la que je bloque) Démontrer alors que =ncarré ( n supérieur ou egal a 1) et que =ncarré - 2n + 2.

pour le a) et le b) c'est juste des démonstration et je ne pense pas vous pénalisez si je ne vous montre pas comment je m'y suis prise car les relations sont l'essentiel mais si vous voulez je peux vous le refaire. Pour le c) j'avais pensé utiliser ma relation
+...+= (n+1)( (+)/2)
mais j'obtiens n(n+1) alors qu'il faudrai juste ncarré. Je pensais que la relaion etait juste mais on ne peut pas suprimer le +1 ? ou alors quel raisonnement dois-je suivre pour démontrer cette égalité ? j'espère que vous pourrez m'aider car j'ai essayé plusieurs autres métodes qui n'aboutissent pas et je ne vois pas comment faire.

[nissart7831]

c) ( c'est la que je bloque) Démontrer alors que =ncarré ( n supérieur ou egal a 1) et que =ncarré - 2n + 2.

Pour le c) j'avais pensé utiliser ma relation
+...+= (n+1)( (+)/2)
mais j'obtiens n(n+1) alors qu'il faudrai juste ncarré. Je pensais que la relaion etait juste mais on ne peut pas suprimer le +1 ? ou alors quel raisonnement dois-je suivre pour démontrer cette égalité ? j'espère que vous pourrez m'aider car j'ai essayé plusieurs autres métodes qui n'aboutissent pas et je ne vois pas comment faire.

Bonsoir,

ton erreur est que tu utilises une formule fausse.

Ta suite commence en fait à (revois les posts précédents). Il n' y a pas de .
Et le terme dans ta formule où tu mets (n+1) doit représenter le nombre de termes de la suite que tu comptes. Et ici, de à , il n'y en a pas n+1 !

Donc refais la bonne formule adaptée à ton cas, et, après calcul, tu verras que tu tombes bien sur le n².

[invite4b0b4f95]

svp un petit peu d'aide j'aimerais juste savoir sur quoi m'appuyer pour ma demonstration ....

[nissart7831]

... et se déduit en utilisant l'expression que tu viens de trouver pour .

[invite4b0b4f95]

J'ai une autre formule pour les termes consécutifs qui me dit que la somme des entiers naturels est égal à ( n(n+1) ) / 2 donc ça devrait me donner des calculs justes mais maintenant en dehors de l'exercice je me demande comment on obtient le n+1 dans l'autre formul je ne vois pas ce que ça change de partir de ou ?

[invite4b0b4f95]

... et se déduit en utilisant l'expression que tu viens de trouver pour .

oui ça j'avais vu c'est avec le a°) qu'on le trouve !

[invite4b0b4f95]

J'ai une autre formule pour les termes consécutifs qui me dit que la somme des entiers naturels est égal à ( n(n+1) ) / 2 donc ça devrait me donner des calculs justes mais maintenant en dehors de l'exercice je me demande comment on obtient le n+1 dans l'autre formul je ne vois pas ce que ça change de partir de ou ?

En faite non elle n'est même pas juste cette propriété car les qui correspondent au nombre de cases ne sont pas consécutifs donc je ne comprend plus pourquoi dans un cas on a (n+1) termes et dans l'autre n ?

[nissart7831]

J'ai une autre formule pour les termes consécutifs qui me dit que la somme des entiers naturels est égal à ( n(n+1) ) / 2 donc ça devrait me donner des calculs justes mais maintenant en dehors de l'exercice je me demande comment on obtient le n+1 dans l'autre formul je ne vois pas ce que ça change de partir de ou ?

Ca change tout de partir de ou !
Car, en supposant que le ait été défini, si tu fais la somme de tes termes de à ou de à , tu vois bien qu'on n'additionne pas le même nombre d'éléments de ta suite.
En effet, dans le 1er cas, c'est , alors que dans le 2ème cas, c'est .

Et dans le cadre de ton exercice, on n'a pas de . En effet, par souci de clarté, on commence à pour que l'indice du terme corresponde au nombre de cases de la ligne n.

La formule pour calculer la somme de termes consécutifs de ta suite est en fait :
S = (nombre de termes que l'on compte). (premier terme + dernier terme)/2

Venons en à la formule que tu as pour la somme des n premiers entiers. C'est

Par rapport à ton exercice, c'est peut être le n+1 qui te trouble.

Voyons comment on trouve cette formule.
Soit () la suite des nombres premiers telle que .
On peut commencer avec . Et on veut calculer :
,

On a n termes à additionner, le premier étant et le dernier est .
En appliquant ce que je t'ai dit plus haut, on a :
CQFD

J'espère avoir été assez clair.

Est-ce que ces explications répondent aussi à ton derner post que j'ai vu après ?

[invite4b0b4f95]

[QUOTE=nissart7831]
Voyons comment on trouve cette formule.
Soit () la suite des nombres premiers telle que .
On peut commencer avec . Et on veut calculer :
,

On a n termes à additionner, le premier étant et le dernier est .
En appliquant ce que je t'ai dit plus haut, on a :
CQFD
QUOTE]

Oui ça répond au dernier post aussi car tu me parles de termes consécutif pour mon exercice et pas seulement d'entiers consécutif .. et est-ce que tu pourrais me faire un exemple avec (n+1) terme car maintenant je ne vois plus comment l'employer ! j'espère pas trop t'en demander !

aussi par rapport à la citation est-ce que pour la sitation je dois toujours remplacer et et juste ceux-la ou aussi pour ne pas citer que deux termes dans ma formules ?

[nissart7831]

est-ce que tu pourrais me faire un exemple avec (n+1) terme car maintenant je ne vois plus comment l'employer !

Ben, un exemple tout simple tiré du précédent sur la somme des n+1 premiers entiers.
Posons () la suite des entiers telle que avec
Tu vois que , , ...

Calculons donc la somme des n+1 premiers entiers, c'est-à-dire :

Tu as donc n+1 termes à additionner. D'après la formule, on a :


Tu peux vérifier qu'en prenant la somme des n premiers entiers (qu'on a vu précédemment) et en lui ajoutant le (n+1)ème entier, soit (n+1), on trouve bien aussi la formule ci-dessus.

aussi par rapport à la citation est-ce que pour la sitation je dois toujours remplacer et et juste ceux-la ou aussi pour ne pas citer que deux termes dans ma formules ?

Je suppose que tu parles de la formule pour additionner les termes consécutifs d'une suite arithmétique.
Dans la formule, on n'a besoin que du premier terme et du dernier terme que tu considères.
Mais tu n'es pas obligé de compter à partir de ou de . Tout dépend de ce que tu cherches.
Par exemple, si tu veux calculer la somme des termes consécutifs(d'une suite arithmétique) de à . Et bien, on aura :


Tu peux aussi t'amuser à voir une utilisation. Si je te dis, calcule la somme des entiers consécutifs de 20 à 30. Fais le 2 manières, l'un en utilisant les suites et donc la formule de la somme, l'autre en additionnant simplement 20 + 21 + 22 + ... 30. Tu verras que ça donne bien la même chose et que c'est plus rapide en utilisant les suites. Et c'est d'autant plus rapide par rapport à la méthode classique que le nombre de termes dans ta somme est élevé.

Ca répond à ta question ?

[invite4b0b4f95]

Ok oui ça répond à ma question je te remercie j'ai bien compris surtout grace au dernier exemple très pertinent.