Nombres premiers, second, troisième,etc, des alignements étranges et dignes d'interêt

[deadcorpse33]

Bonjours mathématiciens et mathématiciennes.
Je me suis lancé dans la création d'un algorythme permettant de retrouver la plupart des nombres premiers.
Grace à un mélange de suites récurentes et de spirale d'Ulam, j'ai retrouvé les polynomes 17+n(n+1) et 41+n(n+1).
Ces polynomes correspondent tout 2 aux diagonales de 2 spirales d'Ulam avec au centre de l'une 17 et de l'autre 41.
En testant ces polynomes, j'ai vu qu'au bout d'un certain rang ces polynomes ne marchait plus.

Je me suis alors mis à chercher un autre moyen plus sur de trouver des nombres premiers.
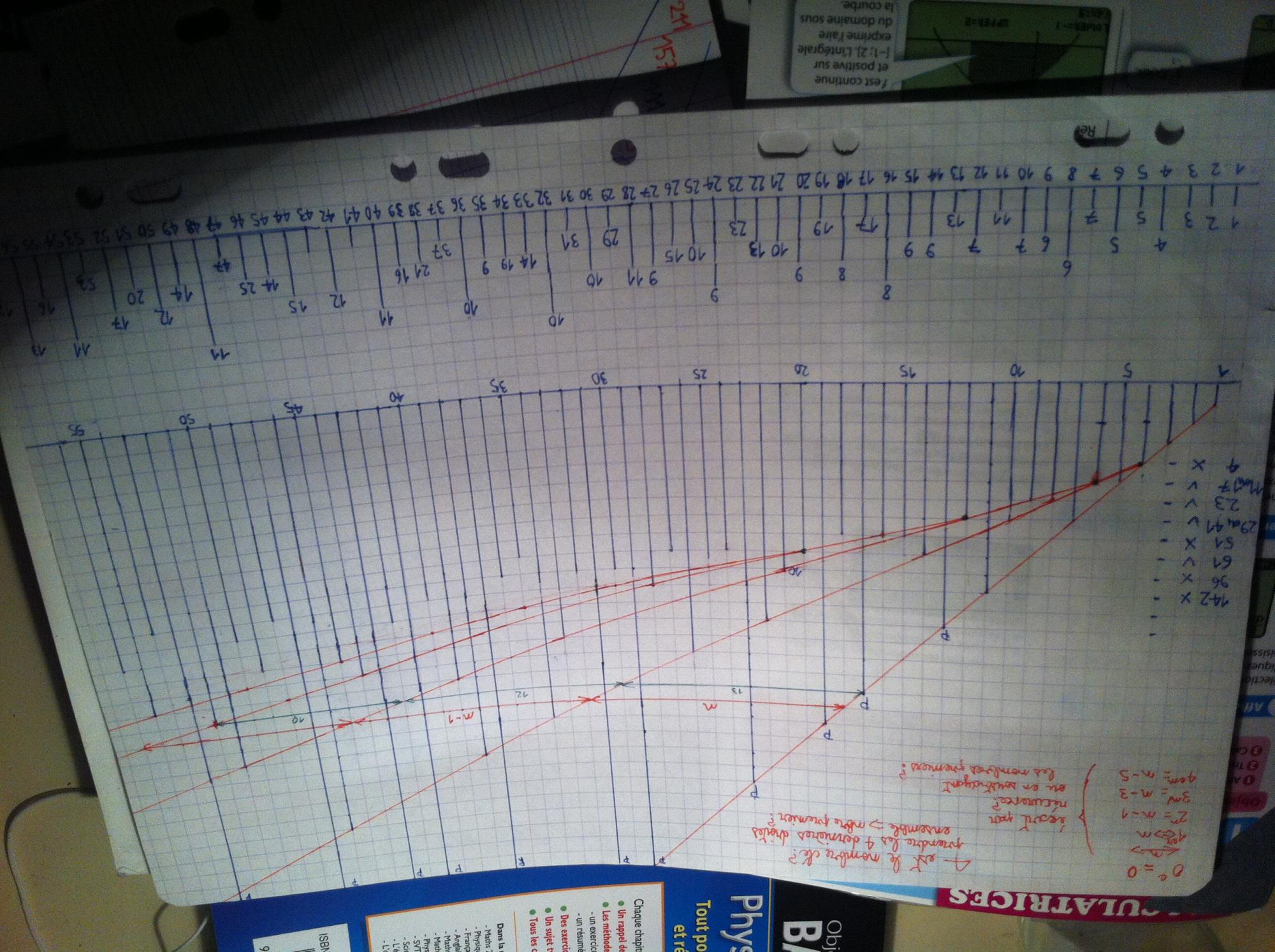
J'ai alors entrepris de faire un histogramme des sommes des facteurs premiers sur une feuille à carreau.
Ex: f(6)=3+2=5 car 3*2=6

J'ai alors observé de curieux alignement de "pointes d'histogramme". Bien sur, comme on peut s'y attendre les nombres premiers constituent une droite d'équation y=x car la somme de leur unique facteur premier est égal à eux même.
Mais qu'en penser de l'alignement des pics de 4,10,14,22,26,34,38,46,etc,
de l'alignement des pics de 6,12,15,21,33,39,51,etc, de l'alignement des pics de 12,16,20,28,44,52,etc.
Ma feuille est trop petite pour continuer cet histogramme mais je suis quasiment sur d'en retrouver une infinité.
Ces alignement forment des droites, en les traçant on obtient alors une sorte de tracé ressemblant à peu près à une racine carré.
En comparant cette ébauche de fonction inconnu à celle d'une racine carré, j'ai alors compris que cette fonction a vraisemblablement pour fonction dérivé la racine carrée à peu de chose près. Je n'ai toujours pas réussi à trouver la formule de cette fonction.

Ces explications doivent vous sembler un peu foireuses mais faites cet histogramme (à baton) chez vous et vous comprendrez à coup sur de quoi je veux parler

Si des choses ont déja été trouvées sur ces aligneents et cette fonction bizarre, indiquez le moi dans les commentaires, cela m'interesse pas mal vu que je suis quasiment certain que ces aligments peuvent servir à prédire l'apparition de certains voire tous les nombres premiers!
-----

[deadcorpse33]

Une photo de l'histogramme.

[topmath]

Bonsoir à tous je suis pas spécialiste des nombres premier , mais y'a ce lien utile Fonction Zêta de Reimann .

Cordialement

[deadcorpse33]

Houla, la fonction que tu viens de me passer est ultra complexe, je suis en terminale S et je n'ai même pas encore étudié le logarythme neperien donc c'est vraiment du charabia pour moi désolé.
Si tu pouvais m'expliquer en vulgarisant un peu cette formule, je t'en serai grès.

[A voir en vidéo sur Futura]

[acx01b]

Ma feuille est trop petite pour continuer cet histogramme

apprends à programmer !

sinon sur la fonction zéta de riemann, oui elle est hyper complexe mais c'est la seule qui ait été trouvée qui permette de mettre dans une fonction (et ses dérivées, son logarithme, etc..) qu'on sait définir formellement des sommes en rapport avec les nombres premiers, genre f(x) = somme des nombres premiers inférieurs à x

[gg0]

Bonsoir.

Mais qu'en (sic) penser de l'alignement des pics de 4,10,14,22,26,34,38,46,etc,

Rien d'exceptionnel, ce sont tous des nombres de la forme x=2p avec p premier donc f(x)=x/2+2
De la même façon, 6, 9, 15, ... sont de la forme x=3p est f(x)=x/3+3.

Tout ça ne nous apprend rien sur les premiers !

Cordialement.

NB : y=x/2+2 et y=x/3+3 sont des équations de droites.