résolution équations cercles tangents

[yoyovento]

Bonsoir,

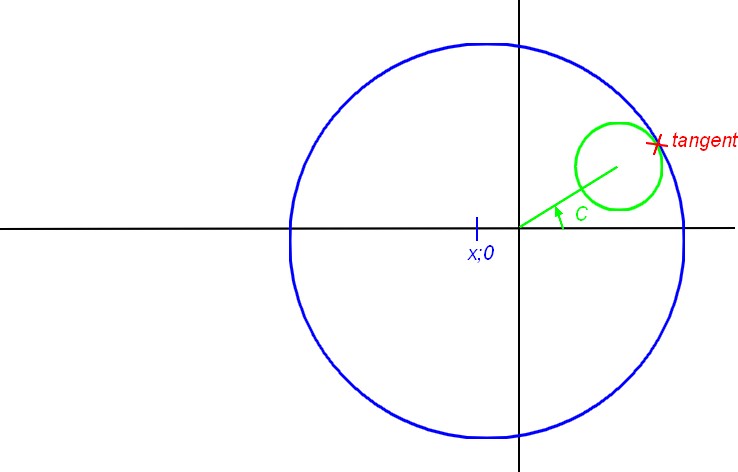
Alors voici mon problème. J'ai un cercle qui tourne autour de (0,0) avec un angle C. Ce cercle "glisse" dans un autre cercle (plus grand) qui a pour coordonnées (-x;0). Le centre du plus grand reste toujours sur les x.
En connaissant les caractéristiaues de cet excentrique (excentricité, diamètre et angle C), je cherche donc x du centre du grand cercle en fonction de son diamètre.
Je ne sais pas si j'ai été clair LOL
J'ai bien cherché l'intersention (x égaux et y égaux) pour ces deux cercles mais j'ai trop d'inconnus....
Quelqu'un peut m'aider ?
-----

[gg0]

Heu...

Une figure ne serait pas de trop. Avec les données connues, les variables, et éventuellement les inconnues.

Cordialement.

[yoyovento]

l'inconnu c'est x, les diamètres sont connus, l'excentricité est connue (trait vert) et C est connu

[yoyovento]

ah ah je crois que j'ai trouvé en voyant ce schéma simplifié.
(1) Rbleu²=(x-xbleu)²+ybleu
(2) cos C = xbleu/(exc+Rexc)-x
(3) sin C = ybleu/(exc+Rexc)

je réinjecte xbleu et ybleu de (2) et (3) dans (1) et tada je tombe sur une identité remarquable du type ax²+bx+c=0.....

à vérifier

[A voir en vidéo sur Futura]

[yoyovento]

Bon ca ne fonctionne pas (ou j'ai dû oublier un signe...)
à 0° je devrais avoir x=exc+Rexc-Rbleu et (x=Rbleu-exc-Rexc à 180°)

[yoyovento]

puf en fait c'est tout simple c'est la bielle manivelle
problème résolu.