questions sur suite et série de fonctions

[Minialoe67]

Bonsoir!

J'ai 2 questions à vous poser:
1) Quand on a montré qu'une suite de fonctions fn(x) converge simplement sur un intervalle mais vers des fonctions différentes selon les valeurs de x, est-ce que forcément elle ne converge pas uniformément?
(par ex: (1-xⁿ)/(1+x²ⁿ) à étudier sur [0,1]
si 0 ≤x<1 Convergence simple (CS) vers 1
si x=1 CS vers 0
mais pas de convergence uniforme (CU) sur [0,1] )

2) Pour montrer la convergence normale d'une série de fonctions, parfois il faut choisir un réel a (car la série de fonctions ne converge normalement (CN) pas sur l'intervalle donné), et montrer que cette série ne converge que sur l'intervalle où l'une des bornes est a. Mais comment choisir a?
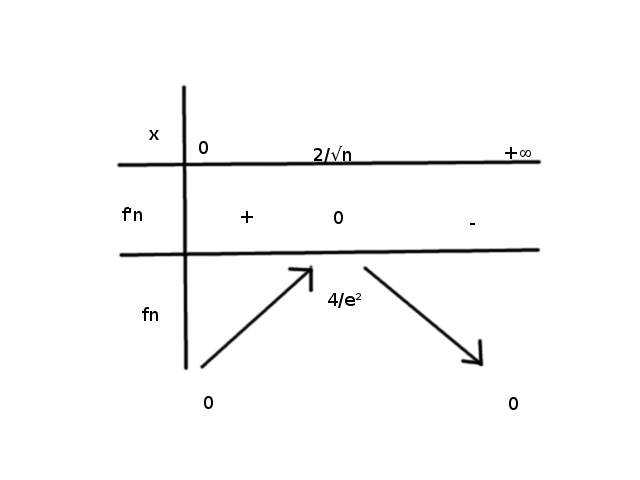
(Par ex: fn(x)=nx²exp(-x√n) à étudier sur R+
Par l'étude de variations, on obtient que la série ne converge pas normalement sur R+.

Par contre si on choisit a > 2/√n , la série CN sur [a,+∞[
Ma question, c'est pourquoi on choisit a > 2/√n et pas a < 2/√n ? )

Merci de me répondre rapidement
-----

[invite34b13e1b]

salut
pour la 1, l'argument sous-jacent est que si une suite de fonctions continues converge uniformement vers une limite f, alors f est continue.
Or tu as montré que sur [0,1] la suite converge (simplement) vers une fonction discontinue. La convergence ne peux donc pas être uniforme.

[Médiat]

Bonjour,

fonctions différentes selon les valeurs de x

Cette formulation n'a pas de sens.