Bonjour,
Dans le cadre d'un projet je dois résoudre analytiquement et numériquement l'EDP suivante.
Mais voilà, j'ai du mal pour le programme MatLab.Je sais que je dois utiliser la méthode des différences finies, mais je n'ai malheureusement pas fait de cours sur cette méthode, et je trouve pas grand chose sur internet pour (x,y,t) (que pour (x,t) et ça marche pas).
Un coup de main serait le bienvenu !
Merci
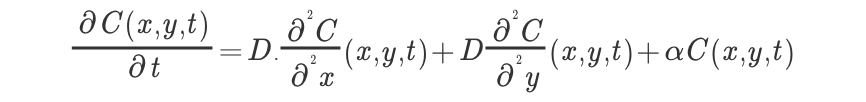
Bonsoir,
L'équation ci-dessus est l'équation de la chaleur avec un terme convectif. Pour la résoudre par différences finies, il faut discrétiser l'espace et le temps en une suite de valeurs espacées de,
pour le temps et,
pour l'espace (idem avec y).
Le problème pour être complet doit préciser les conditions initiales et les conditions aux limites. On obtient un système d'équations linéaires sur les
Bon courage
Merci bien !
Je vais essayé de me débrouiller avec ça !
Bonjour,
Au final je me retrouve bloqué (du moins je crois. C'est un projet obligatoire, mais les maths ne sont pas du tout ma spécialité !).
Alors je pose mon équation un fois les termes en temps et espace discrétisés, avec mes conditions telles que :
- Condition initiale : à t=0, C(x,y,0)=0
- Conditions aux limites : (je travaille dans un carré de longueur L) C(0,y,t)=C(L,y,t)=C(x,0,t)=C(x ,L,t)=0
Mon problème est très simplifié, mais malgré ça j'arrive pas a savoir si le resultat que trouve est juste.
Je tombe au final sur C(x,y,Δt) = 0, ce qui pour moi semble faux.
Mon problème physique est la diffusion de microparticules au alentour d'une ville (source : pots d'échappements), et le terme C(x,y,Δt) ne devrai pas être nul car il y a création de particule permanent et le pas Δt n'est pas nul.
Je me trompe peut être sur l'interpretation physique du C après, comme dit précédemment, c'est pas trop mon domaine d'expertise.
avec ces conditions initiales ce n'est pas difficile à résoudre analytiquement !Envoyé par tompouce222
tu peux le faire ?
