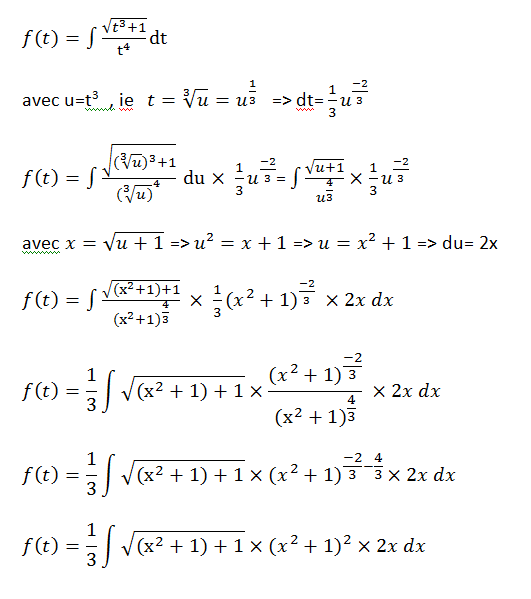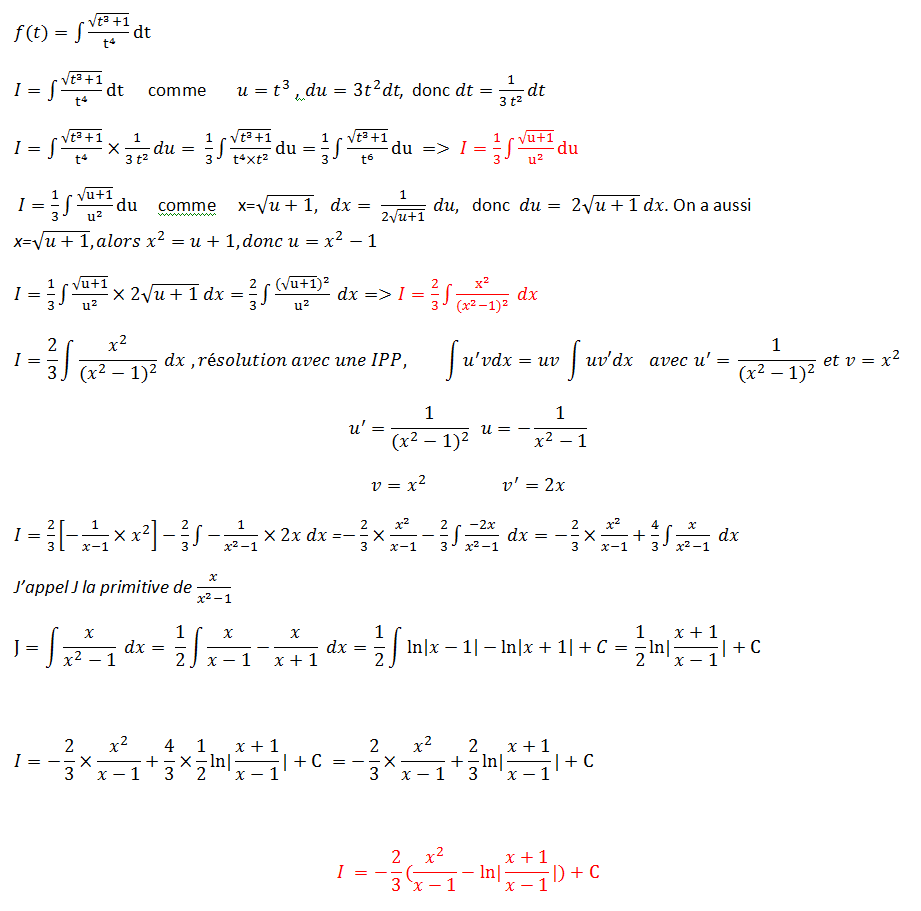Bonjour
Je ne suis pas très fort en math et je dois calculer une primitive. La primitive est la suivante:
Je dois calculer une primitive de cette fonction à l'aide d'une intégration par partie avec 2 changements de Variable successifs u=t^3 et x=racine(u+1)
Pourriez-vous m'aider dans les démarches à réaliser pour calculer cette primitive ?
Merci d'avance
Je viens de voir que l'image de la fonction n'est pas encore passé : en attendant
f(t)= (racine(t^3+1))/t^4
Bonjour.
Comme la méthode t'est donnée et qu'il s'agit d'une application immédiate des méthodes de cours, à toi de faire le calcul et de nous le présenter. Si à u_n moment ça bloque ou si tu vérifies que ton résultat est faux, on pourra te dire ...
Rappel : http://forums.futura-sciences.com/ma...ces-forum.html
Cordialement.
Bonjour gg0
Je suis parti dans cette direction
f(x)=√(t^3+1)/t^4 Avec le premier changement de variable u=t3 => f(x)=(u+1)/u² = √(u+1)/u puis le second changement de variable x=√(u+1) => f(x)=x/(x²-1)
De la j’ai commencé à cherché la primitive :
F(x) = 1/2 ∫(1/(x-1)-1/(x+1))dx+C= 1/2 (ln |x-1|-ln |x+1|)+C=1/2 ln|(x-1)/(x+1)|+C
Ensuite j’ai remplacé x pour retrouver u et u pour retrouver t
F(x) = 1/2 ln|(x-1)/(x+1)|+C=1/2 ln|(√(u+1)-1)/(√(u+1)+1)|+C= 1/2 ln|(√(t^3+1)-1)/(√(t^3+1)+1)|+C
F(x) = 1/2 ln|((t^2+1)-1)/((t^2+1)+1)|+C
Pour moi la primitive était résolus mais je n’ai pas fais d’ipp donc … donc je pensais faire une IPP à partir de là, avec u=1/2 et v’ le reste ln … .
Mais je ne suis vraiment pas sur d’être sur le bon chemin
Effectivement,
il n'y a pas besoin d'intégration par parties, puisque les deux changements de variable donnent une fraction rationnelle à intégrer. Mais on peut effectivement en utiliser un pour intégrer cette fraction rationnelle.
Par contre, tes calculs sont faux. Le premier changement de variable n'a pas été fait correctement, sur l'intégrale; le deuxième ne me semble pas correct non plus.
Revois la méthode (on change l'intégrale, pas la fonction).
Cordialement.
Dernière modification par gg0 ; 05/04/2014 à 19h06.
j'ai recommencé les calculs, voilà m'a démarche:
f(t)=√(t^3+1)/t^4
avec u=t3 , ie t=∛u=u^(1/3) => dt= 1/3 u^((-2)/3)
f(t)=∫(√((∛u)^3+1))/(∛(u))^4 du × 1/3 u^((-2)/3)= ∫(√(u+1))/u^(4/3) × 1/3 u^((-2)/3)
avec x=√(u+1) => u²=x+1 => u=x²+1 => du= 2x
f(t)=∫(√((x^2+1)+1))/((x^2+1)^(4/3)) × 1/3 (x^2+1)^(-2)/3) ×2x dx
f(t)=1/3 ∫√((x^2+1)+1)×((x^2+1)^(-2)/3))/((x^2+1)^(4/3)) ×2x dx
f(t)=1/3 ∫√((x^2+1)+1)×((x^2+1)^((-2/3)-(4/3)))×2x dx
f(t)=1/3 ∫√((x^2+1)+1) × (x^2+1)^2 × 2x dx
Par rapport à la première fois est-ce que c'est plus juste ?
Merci d'avance
Cordialement.
(ps =j'ai collé l'image des calculs ci dessus (plus lisible)
J'ai un doute...Envoyé par Xenezis
oui pardons x=√(u+1) => x²=u+1 => u=x²-1 => du= 2x
j'ai rectifié f(t)
Bonjour.
Que tu peux compliquer les choses ! En n'appliquant pas strictement les règles.
Déjà, l'intégrale n'est pas f(t) puisque c'est f(t) qu'on intègre.
Ensuite dt= 1/3 u^((-2)/3) est faux. Ce qui est correct c'est dt= 1/3 u^((-2)/3) du
Puis l'écriture ∫(√((∛u)^3+1))/(∛(u))^4 du × 1/3 u^((-2)/3) pour l'intégrale est malsaine car "du" marque la fin de la fonction à intégrer.
Ensuite, tu ne simplifies pas cette écriture qui s'arrange pourtant bien, tu pars dans une expression compliquée.
Cerise sur le gâteau, une énormité : " u²=x+1 => u=x²+1"
Inutile qu'on essaie de t'aider si tu écris de telles âneries. Il n'est pas acceptable, à ton niveau, de jouer avec les écritures sans réfléchir ! les maths utilisent des transformations d'écritures qui correspondent à des règles bien précises. Toute autre transformation d'écriture, même si elle te plaît, est potentiellement une erreur.
Bon, je t'aide à commencer, avec un petit truc simple :
Comme
A toi de continuer en appliquant les règles ...
Bonsoir à tous :
Pour ma part je continue le travail de gg0, on essayant de ramener cette fonction
On posant
Notre intégrale devient :
Cordialement
Topmaths,
ce n'est pas l'habitude ici de faire le travail à la place des autres. j'ai guidé Xenesis pour faire proprement son travail, ce n'était pas pour que tu le fasses.
Oui je comprend gg0 mais , justement le travail n'est pas terminé et je lui laisser une belle partie de ce ci .
Cordialement
Bonsoir gg0 et topmath
Tous d’abord gg0 désolé de t'avoir mis hors de toi sur mon premier retour .... je me rends compte que je faisais n'importe quoi et que je n'avais pas compris la finalité du changement de variable.
Topmath j'ai vue après coup que j'avais réussi à avoir un peut près le même raisonnement que toi pour le second changement de variable, merci de ton retour.
Je pense avoir fini l'exercice. Vous trouverez ci-dessous l'exercice que j'ai retravaillé:
Cordialement
Bonjour à tous :
Je crois qu'il y'a une petite erreur de frappe dans la pièce photos du message précédant, puisque le résultat est juste :
Je corrige :
Cordialement
