Calcul d'aire - cardioide ?

[invite82bd8b9c]

Bonjour,

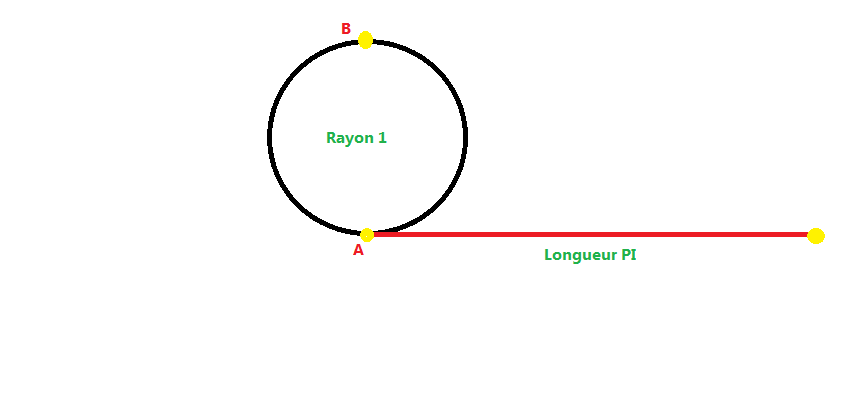
J'ai mis un dessin en pièce jointe pour mieux comprendre.
Je voudrais connaitre l'aire de la figure décrite par la corde rouge de longueur PI.
En sachant que celle-ci est fixée au point A et qu'elle est "bloquée" par le cercle de rayon 1. (c'est à dire que pour aller en B, elle est obligée de suivre le chemin du cercle etc).

La courbe décrite me fait penser à une cardioide de longueur 8a et d'aire 3/2 * pi * a^2 avec a = 0.5 * (1+ pi)

Qu'en pensez vous ?

Merci


-----

[invite82bd8b9c]

Je ne sais pas si j'ai été très clair. La corde en rouge est fixée en A et elle pivote autour de A pour tous les angles du plan.

[gg0]

Bonjour.

Il s'agit plutôt d'une développante de cercle. Voir par exemple wikipédia.

Cordialement.

[invite82bd8b9c]

Ok, merci.

[A voir en vidéo sur Futura]

[invite82bd8b9c]

Je comprends bien le principe de la développante mais je bloque pour le calcul de l'aire.

Ici j'aurai 2 * l'aire de du début de développante jusqu'à intersection avec l'axe vertical. Mais comment exprimer cela ?

[gg0]

J'ai tout oublié du calcul d'aires limitées par des courbes paramétrées. désolé !
A ma décharge, je n'ai plus fait ça depuis 1970.

[breukin]

On devrait pouvoir s'en sortir en paramétrant par l'angle de l'arc de cercle (allant de 0 à ), en calculant les coordonnées du point jaune non désigné par une lettre en fonction de cet angle (pour 0, il vaut (, 0) ; pour , il vaut (0, 2).
Pour , on a qui est "consommé" le long de l'arc de cercle, et il reste un segment de longueur , de pente , et commençant au point (sin, 1-cos).

[invite82bd8b9c]

Merci pour l'info, j'ai finalement préféré le calcul "bourrin" par informatique

[breukin]

Finalement, ce n'est pas trop compliqué.
Le point jaune a pour coordonnées :


Il faut donc calculer :


La fonction à intégrer peut s'écrire :


On s'en sort en intégrant par parties en dérivant les parties polynomiales et en intégrant les lignes trigonométriques.

Finalement, je trouve sauf erreur .
En enlevant le demi-cercle, il reste .

[invited3a27037]

bonjour

Dans le cas général, pour calculer l'aire d'une zone délimitée par une courbe paramétrée, on peut utiliser le théorème de Green-Riemann et se ramener au calcul d'une intégrale curviligne. http://fr.wikipedia.org/wiki/Th%C3%A...culs_d.27aires

Il y a aussi cette formule:

ou O est un point quelconque à l'intérieur, c la courbe et M(t) le point qui se déplace sur la courbe en fonction du paramètre t.

Le est l'aire d'un triangle élémentaire de sommets 0, M(t) et M(t+dt)

Il faut quand même regarder de près ce qui se passe s'il y a des boucles.

[invited3a27037]

pour cette dernière formule



après réflexion, je pense qu'elle ne fonctionne que s'il n'y a qu'un seul point d'intersection entre les rayons issus de O et la courbe c.

Prendre la norme après l'intégrale devrait améliorer la situation

[invited3a27037]

Finalement, je trouve sauf erreur .
En enlevant le demi-cercle, il reste .

Je pense qu'il y a une erreur quelque part.
J'ai fait un schéma sous géogebra et j'ai mesuré l'aire en créant un polygone qui suit au mieux la courbe et je trouve une aire de 6.73 avec le demi-disque inclus alors que tu trouves (pi^3)/6+pi/4 = 5.95. La différence représente 20 carreaux de la grille, c'est trop.

Si quelqu'un sait comment mesurer une aire sous une courbe dont on a pas l'équation avec géogébra, la courbe étant obtenue comme trace d'un point, je suis preneur.

[invited3a27037]

oui, petite erreur de pi/4

http://www.wolframalpha.com/input/?i...\theta+d\theta

[breukin]

Effectivement, je reviens de faire le calcul, sans Wolfram, avec comme primitive :


Donc et donc sans le demi-cercle.