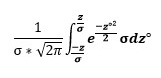Intégrale gaussienne

[petitpaume]

Bonjour,

je poste ce message car j'ai un gros soucis avec une intégrale qui me donne mal à la tête depuis quleques
jours.

En fait dans l'exercice il y a une cible de fléchette et on reporte différentes valeurs du point d'impact de la flèche
et une obtient une gaussienne de fonction fonction gaussienne.png. On nous demande alors combien doit être ici z
pour avoir 75% de toucher la cible entre m-z et m+z
Je voudrais intégrer cette loi normale d'une gaussienne intégrale gaussienne.png.
Je voudrais l'intégrer sur un intervalle m-z; m+z où m est la moyenne et z un déplacement quelconque.
Un intervalle qui doit correspondre à la probabilité de 75 %.
Donc l'intégrale de la fonction gaussienne sur l'intervalle [m-z; m+z] doit être égale à 0.75.

J'avais essayé avec un changement de variable X= (x-µ)² ce qui donne dX=(2x-2µ)dx
mais si je mets ça dans mon intégrale j'ai des x qui se balade alors que je veux que ça dépende que de X
Est ce une bonne méthode le changement de variable ?
ou si vous en avez une autre ?

Merci d'avance pour vos réponses
-----

[gg0]

Bonjour.

La fonction n'a pas de primitive exprimable simplement. On utilise le passage par la loi Normale centrée réduite et des tables ou des calculs approchés faits par des logiciels ou calculettes.

Cordialement.

[gg0]

si je mets ça dans mon intégrale j'ai des x qui se balade

Alors tu n'appliques pas la méthode du changement de variable. Qui est de calculer dx en fonction de dX, de remplacer, de remplacer (x-µ)² par X et de modifier les bornes.

Par contre, en posant où Z est ta variable aléatoire initiale, on obtient

Et Z* suite une loi simple dont on a des tables, et qui est calculée par certaines calculettes, les tableurs, et les logiciels scientifiques ou de statistiques. Voir un cours de base sur la loi Normale.

Cordialement.

[petitpaume]

Merci pour tes réponses

Par contre je me suis trompé m c'est la moyenne µ mais je pense que t'avais compris
En faisant ton changement de variable Z* = (Z-µ)/𝞂
J'arrive à 1/(σ*√2π) ∫e^((-Z²)/2) σdZ* est-ce correct ?

Par contre moi je trouve -z𝞂<z*< z𝞂
N.B : Je pense que tu t'en est rendu compte-rendu mais je ne suis pas très doué en maths

[A voir en vidéo sur Futura]

[petitpaume]

Dans l'intégrale c'est Z* et c'est plutôt -1/2*(Z*)²

[gg0]

Non, non,

Z est une variable aléatoire. Ne pas confondre un changement de variable aléatoire avec un calcul d'intégrale par changement de variable (numérique). Dans mon message, il y a bien un Z (variable aléatoire Normale) et un z (valeur numérique).

Cordialement.

[gg0]

Je remets ma proposition(classique) rectifiée :
Par contre, en posant où Z est ta variable aléatoire initiale, on obtient

Et Z* suite une loi simple dont on a des tables, et qui est calculée par certaines calculettes, les tableurs, et les logiciels scientifiques ou de statistiques. Voir un cours de base sur la loi Normale.

Cordialement.

[gg0]

Sinon,

ton changement de variables, dans l'intégrale, aux notations près est presque correct : Il manque les bornes, qui ont modifiées. Il donne d'ailleurs le même résultat que le cahngement sur la variable aléatoire (heureusement !).

[petitpaume]

Donc si je marque ça
c'est juste ?

sinon j'ai trouvé (sur internet) que les fonctions de ce type avait une intégrale de √π mais pour en intervalle
de - à + l'infini mais ce n'est pas vraiment l'intervalle que je cherche.
Et toutes ces intégrales passaient par des coordonnées polaires.