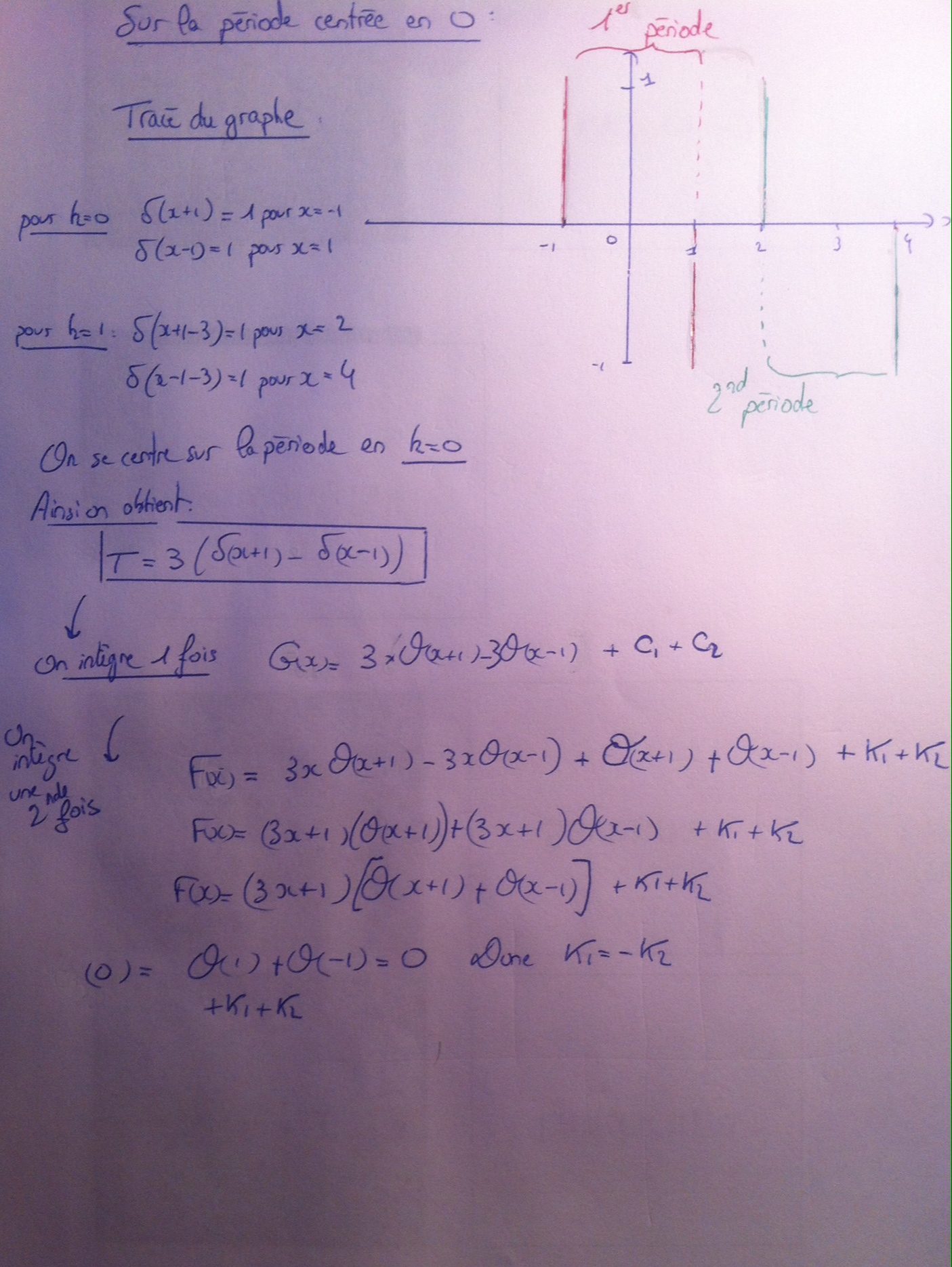
Problème math distributions
Discussions similaires
-
Par invite88ce7116 dans le forum Dépannage
Réponses: 4
Dernier message: 27/12/2014, 05h33
-
Par inviteec33ac08 dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 19/06/2014, 02h56
-
Par invitefb95b365 dans le forum Mathématiques du supérieur
Réponses: 15
Dernier message: 24/12/2012, 14h11
-
Par invite1e842170 dans le forum Mathématiques du supérieur
Réponses: 1
Dernier message: 05/12/2010, 10h48
-
Par invite176531fd dans le forum Mathématiques du supérieur
Réponses: 5
Dernier message: 24/04/2007, 18h17






 donnent le résultat 0. J'ai réalisé à la suite de ton message que si on accepte que les séries qu'on écrit converge, cette remarque n'a aucune importance. mais évidemment, utiliser une série sans savoir si elle converge est dangereux.
donnent le résultat 0. J'ai réalisé à la suite de ton message que si on accepte que les séries qu'on écrit converge, cette remarque n'a aucune importance. mais évidemment, utiliser une série sans savoir si elle converge est dangereux.