Sous ensemble infini

[noureddine2]

Salut , je sais qu'un sous ensemble d'un ensemble infini peut lui aussi être infini .
mais les deux ne sont pas identiques au niveau de la taille .
ma question est :
c'est quoi la différence de taille par exemple entre l'ensemble Z et l'ensemble R ? merci .
-----

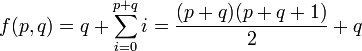
[Médiat]

Bonjour,

Avant de vous répondre, il faut que j'insiste, une fois de plus, le "nombre d'éléments d'un ensemble" n'est pas une notion mathématique, la notion mathématique qui s'en rapproche est le cardinal, et on a Card(N) = Card(Z) = Card(Q) < Card(R) = 2^Card(N).

Sinon vous pouvez regardez là : http://forums.futura-sciences.com/ma...-ensemble.html, ou là : http://www.math.uni-hamburg.de/home/...ides/forti.pdf

[noureddine2]

Bonjour,

Avant de vous répondre, il faut que j'insiste, une fois de plus, le "nombre d'éléments d'un ensemble" n'est pas une notion mathématique, la notion mathématique qui s'en rapproche est le cardinal, et on a Card(N) = Card(Z) = Card(Q) < Card(R) = 2^Card(N).

merci , quand je regarde ce lien
https://fr.m.wikipedia.org/wiki/Card...mathématiques)

L'union et l'intersection de deux parties A et B de E sont reliées par la formule :

je remplace À et B par Z et Q , on a :

je n'arrive pas à voir comment Card (Z) = Card (Q)

[Médiat]

Ce qui vous donne

[A voir en vidéo sur Futura]

[Schrodies-cat]

En ce qui concerne la différence de cardinalité entre N et R, elle a été obtenue par Cantor avec l'argument suivant:
https://fr.wikipedia.org/wiki/Argume...nale_de_Cantor
Par contre N, Z, Q, N^2, Z^2 etc ont le même cardinal, qui est celui du dénombrable.
Il faut se méfier des opérations sur les cardinaux, elles n'ont pas toutes les propriétés des opérations usuelles ainsi, par exemple:
Si A et B sont infinis et de même cardinal, Card(A)+Card(B) = Card(A). Ce qui est le cas avec les ensembles cités dans le message ci-dessus qui sont tous dénombrables. Je suis par contre perplexe en ce qui concerne la définition de la soustraction de deux cardinaux dans le cas infini.
C'est Georg Cantor qui a fondé l'étude des cardinaux infinis.

[Tryss]

Je suis par contre perplexe en ce qui concerne la définition de la soustraction de deux cardinaux dans le cas infini.

Sans être un spécialiste, il me semble que l'on peut dire :

Soit et deux cardinaux.

Alors si , , ici ça ne pose pas de problème

Par contre si , on aurait que , et là c'est le drame

[Schrodies-cat]

Je vais préciser la chose:
N est en bijection avec les entiers naturels pairs par n->2*n et avec les entier naturels impairs par n->2*n+1.
Ces trois ensemble ont donc le même cardinal, appelé Aleph1.
On a donc card(entiers)=card(pairs) + card (impairs) (l'union étant disjointe), d'ou, si on définit une soustraction:
card (entiers)-card (pairs)= card(impairs) , et donc compte tenu de ce qui a été dit plus haut:
Aleph1-Aleph1= Aleph1 ... Hum , c'est déjà inquiétant; mais d'autre part:
card(entiers )= card(entiers) +card(vide) donc
card(entiers)-card(entiers)=card(vide) soit:
Aleph1-Aleph1=0 !
Définir une soustraction entre cardinaux infinis conduit donc a des contradictions.

[Médiat]

N est en bijection avec les entiers naturels pairs par n->2*n et avec les entier naturels impairs par n->2*n+1.
Ces trois ensemble ont donc le même cardinal, appelé Aleph1.

Non, c'est

[Schrodies-cat]

Effectivement, toujours le même piège:
0 est le premier entier naturel, 1 est le deuxième entier naturel, 2 est le troisième entier naturel ...
Mais je m'égare dans la théorie ordinale, qui n'est pas le sujet ...

[noureddine2]

et on a Card(N) = Card(Z) = Card(Q) < Card(R) = 2^Card(N).

je cherche une démonstration qui montre cette égalité entre Card de N et Z et Q.
merci.

[PlaneteF]

Bonsoir,

je cherche une démonstration qui montre cette égalité entre Card de N et Z et Q.

Check this out:

https://fr.wikipedia.org/wiki/Ensemble_d%C3%A9nombrable


Cordialement

[Médiat]

Soit définie par doit être une bijection.

Soit définie par (où p, q) est le représentant irréductible d'un rationnel positif), est une injection, en trouver une dans l'autre sens est trivial

[pm42]

Pour compléter ce que dit Mediat, une autre façon de voir est de créer les bijections visuellement : pour Z, tu comptes les éléments. Tu commences par 0, puis 1, puis -1, puis 2, puis -2...
Et tu vois que tu arrives à tous les compter les un après les autres et qu'en faisant, tu crées une bijection. Donc Card(N) = Card(Z).

C'est la version "du pauvre" de la fonction de Mediat au dessus.

Pour Q, tu prends un quart de plan et tu dis que chaque point aux coordonnées entières représente un rationnel. Tu peux aussi les compter en te déplaçant en spirale. Donc tu es sur que Card(Z) <= Card(N)
Et comme Z contient N, Card(Z) >= Card(N), on voit que Card(Z) = Card(N).
Ce n'est pas rigoureux, juste une illustration mais qui permet ensuite de construire la bijection avec un peu de travail.

[Schrodies-cat]

Tu peux également utiliser la bijection entre N^2 et N définie par

Vu comme ça, c'est un cadeau empoisonné, mais il suffit d'écrire les premières valeurs de f en fonction de a et b sur un quadrillage pour comprendre comment ça marche.
Source:https:https://fr.wikipedia.org/wiki/Ensemble_dénombrable.
Tu a donc une bijection entre N et N^2, dont tu peux déduire une bijection entre N et Z^2
La difficulté est que la surjection entre Z^2 et Q définie par (a,b)->a/b n'est pas injective (et pas définie partout ...).
Toutefois, en partant de la fonction surjective entre N et Q définie par ce qui précède, tu peux obtenir par récurrence une suite bijective entre N et Q en prenant le soin d'éviter les cas ou la fonction n'est pas définie et les doublons.

L'utilisation de la comparaison (=< etc) de cardinaux dans les démonstration doit être évitée à un niveau élémentaire, beaucoup de résultats qui semblent évidents demandant en fait des démonstrations un peu techniques.
(Il est vrai qu'avec le théorème de Zorn, tout devient évident ... )

[noureddine2]

peut être que le cardinal n'est pas la meilleure méthode pour comparer des ensembles infinis .
alors je propose d'utiliser d'abord des segments fermés
https://fr.m.wikipedia.org/wiki/Segment_(mathématiques)
par exemple de valeur absolue inférieure ou égale à 100 .
[ 0 , 100 ] dans N
[ -100 , 100 ] dans Z
[ -100 , 100 ] dans Q
[ -100 , 100 ] dans R
je me demande ce que va donner l'utilisation du cardinal pour comparer ces segments fermés .

[gg0]

Toutes ces questions sont bien connues, et même toi, tu peux répondre pour les deux premiers cas. Il est classique que le cardinal de "[ -100 , 100 ] dans Q" est celui de N et Q, et le cardinal de [ -100 , 100 ] dans R" est celui de R. Dans les deux cas, l'utilisation de la fonction x--> 1/x permet de montrer qu'à quelques valeurs près, il y a une bijection. Et si E est un ensemble infini, et a un des ses éléments, E-{a} est de même cardinal que E.

Comme toutes ces questions sont classiques, il serait bon que tu étudies la théorie des ensembles (*) avant de continuer à poser des questions qui y sont traitées de façon bien plus générales.

Cordialement.

(*) par exemple dans le cours de Dehornoy qu'on trouve sur Internet.

[Médiat]

[noureddine2]

et on a Card(N) = Card(Z) = Card(Q) < Card(R) = 2^Card(N).

j'ai vu dans ce lien
http://www.sciences.ch/htmlfr/arithm...nsembles01.php

Ce problème se résout d'une façon assez étonnante. D'abord, en 1938, un des plus grands logiciens du 20ème siècle, Kurt Gödel, démontra que l'hypothèse de Cantor n'était pas réfutable, c'est-à-dire qu'on ne pourrait jamais démontrer qu'elle était fausse. Puis en 1963, le mathématicien Paul Cohen boucla la boucle. Il démontra qu'on ne pourrait jamais non plus démontrer qu'elle était vraie!!! Nous pouvons conclure à juste raison que Cantor avait perdu la raison à chercher à démontrer un problème qui ne pouvait pas l'être.

je pense que cette égalité :
Card(N) = Card(Z) = Card(Q) < Card(R) = 2^Card(N).
n'est pas réfutable donc presque non scientifique .
donc je veux chercher une autre méthode comme les opérations des limites infinis .
est ce qu'on peut utiliser les limites infinis pour comparer entre les ensembles infinis ?
je vais voir ce lien :

http://tanopah.jo.free.fr/ADS/bloc2/limitefct3.html

[Médiat]

Vous confondez hypothèse du continu et arithmétique cardinale de base.

Vous devriez commencer par étudier la théorie des ensembles.

[pm42]

je pense que cette égalité :
Card(N) = Card(Z) = Card(Q) < Card(R) = 2^Card(N).
n'est pas réfutable donc presque non scientifique .
donc je veux chercher une autre méthode comme les opérations des limites infinis .

Je confirme ce que dit Mediat et je me permet de suggérer qu'avant de mettre en doute ce qui a pourtant été précisément expliqué ici et de "chercher une autre méthode", il vaudrait mieux commencer par comprendre.

[PlaneteF]

Bonsoir,

(...)
n'est pas réfutable donc presque non scientifique .
(...)

? ?

Je crois que tu mélanges un peu tout là, ... et il me semble nécessaire que tu reprennes tous ces concepts à la base.

Cordialement

[noureddine2]

je met ce lien sur le développement décimal pour chercher cette histoire de aleph-0
https://fr.m.wikipedia.org/wiki/Développement_décimal
Je cherche une démonstration de cet aleph-0 .

[Schrodies-cat]

peut être que le cardinal n'est pas la meilleure méthode pour comparer des ensembles infinis .
alors je propose d'utiliser d'abord des segments fermés
https://fr.m.wikipedia.org/wiki/Segment_(mathématiques)
par exemple de valeur absolue inférieure ou égale à 100 .
1:[ 0 , 100 ] dans N
2:[ -100 , 100 ] dans Z
3:[ -100 , 100 ] dans Q
4:[ -100 , 100 ] dans R
je me demande ce que va donner l'utilisation du cardinal pour comparer ces segments fermés .

1:fini = 101
2:fini = 201
3:dénombrable
4:continu