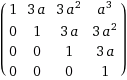Bonjour,
J'ai besoin d'aide. J'ai une matrice 4x4 :
1 a 0 0
0 1 a 0
B = ( 0 0 1 a )
0 0 0 1
Calculer B2,B3 et B4 puis Bn
Comment ce résultat peut-il se généraliser pour une matrice de la même forme mais de taille quelconque ?
Je sais qu'il faut utiliser le binôme de newton pour démontrer la récurrence, mais je suis perdu.
Merci d'avance.
Je suppose que par sa légende, les termes Bn signifient, B élevé à la puissance n.
Vous pouvez utiliser le lien suivant ci-dessous:
http://www.wolframalpha.com/input/?i...ons.theMatrix3---.*--
Pour B2:
Pour B3:
Sucessivement...
Une petite erreur ci-dessus.
S'il vous plaît lire B3 comme la matrice suivante:
Bonjour,
Je vous remercie pour votre retour rapide.
En fait, ce que je n'arrive pas à comprendre, c'est comment on applique le binôme de newton pour prouver la récurrence après avoir fais la matrice B^4.
Merci d'avance
Si nous continuons à calculer la matrice d'ordre 4, il ne semble pas vraie relation avec triangle de Pascal:
Je peux me tromper, mais après avoir fait une brève induction algébrique, je suis capable de déduire la forme générale d'une matrice 4x4 avec les paramètres que vous avez fournis (s'il vous plaît examiner s'il est correct ):
Voici la réponse de l'enseignant :
B^n :
1 C'n a C²na² C^3na^3
0 1 C'na C²na²
0 à 1 C'na
0 0 0 1
Je suis completement perdu, et je ne sais pas comment il a fait pour parvenir jusque là.
Bonsoir.
On reconnait les coefficients du tableau de Pascal dans les puissances 2, 3 et 4, et pas ce qu'écrivait André_teprom. Il ne reste plus qu'à faire la preuve par ré"currence que cette formule est juste, en multipliant Bn par B.
Bon travail !
Dernière modification par gg0 ; 08/12/2015 à 22h52.
Bonsoir,
En effet, quand je regarde le tableau de pascal, je reconnais les lignes pour les puissances 2,3 et 4. Par contre, ce que je ne comprends pas, c'est comment forme t'on les Cn etc... Je n'arrive pas à comprendre la méthode après avoir fais la matrice à la puissance 4.
Cordialement.
Tant que tu ne mets pas en place la démonstration par récurrence, tu es dans le cas particulier qui cache la règle. Mets-toi vraiment au travail (c'est ton exercice).
Juste rappeler que la matrice présentée en post #6 ne peut pas être tout à fait exact.
Il était juste une conclusion rapide, qui, comme je l'ai mentionné, aurait besoin d'être révisé pour confirmer sa véracité.
Aussi, je n'ai pas revu le calcul effectué sur le lien ci-dessus.
En raison de certaines incohérences - nouvellement découverts - il est susceptible d'être incorrect.
Quoi qu'il en soit, il est votre travail maintenant decouvert qu'est ce qui c'est passé.
Je pense que avec ces informations vous pouvez commencer á partir de ce point.
La fascination de la mathématique est que nous pouvons déduire le même résultat a pris de diverses manières.
