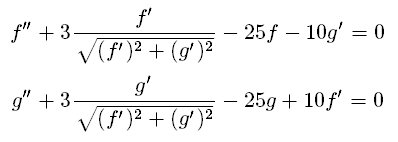Equations différentielles couplées

**kdjender** · 14/03/2016, 17h49

Bonjour à tous, j'ai un système de deux équations différentielles couplées que je n'arrive pas à résoudre, merci de bien vouloir m'aider à le résoudre ou à me donner une alternative.

Sans titre.png

Sans titre.png

Bonsoir, j'ai déjà posté ce système d'équations différentielles sur ce forum pour espérer trouver une solution analytique mais pas de chance. Aussi je vous demande de m'aider si possible pour savoir quelle méthode utiliser pour résoudre numériquement ces équations différentielles. Je tiens à préciser que f et g sont fonction du temps (c a d f(t) et g(t)). Merci.

**God's Breath** · 14/03/2016, 17h55

Ce système me donne furieusement envie de poser $\text{[math]}$ , mais j'ai l'impression que cela n'arrange pas vraiment les choses.

azizovsky · 14/03/2016, 18h15

si on pose $\text{[math]}$ , l'équation s'écrit ?:

$\text{[math]}$

x=f et y =g

**kdjender** · 14/03/2016, 18h53

Donc du coup, toujours pas de solution ?

J'avais essayé avec z=f+ig mais il y a le module complexe |z| qui gêne la ou il y a la racine carée. :/

A voir en vidéo sur Futura · Aujourd'hui

azizovsky · 14/03/2016, 21h30

on peut l'écrire $\text{[math]}$ avec $\text{[math]}$ et $\text{[math]}$ (un cosinus directeur...)

azizovsky · 14/03/2016, 22h22

Envoyé par azizovsky

on peut l'écrire $\text{[math]}$ avec $\text{[math]}$ et $\text{[math]}$ (un cosinus directeur...)

comme d'ab ....(des corrections) $\text{[math]}$

**kdjender** · 17/03/2016, 11h21

Rebonjour, bon apparemment pour trouver une solution analytique à ce système d’équations diff relève de l'impossible, comment pourrai je les résoudre numériquement ? Avec quelle méthode ? Merci.

**kdjender** · 17/03/2016, 11h36

Envoyé par azizovsky

comme d'ab ....(des corrections) $\text{[math]}$

D'après vous si cos(alpha) s’écrit de la forme que vous avez indiqué, quelle serait la forme de cos(beta) ? Est ce que c'est suffisant pour les résoudre analytiquement ?

azizovsky · 17/03/2016, 14h33

le $\text{[math]}$ à la même forme que $\text{[math]}$ , je me suis arrêter à l'équation

:

$\text{[math]}$ j'ai remplacé $\text{[math]}$ et j'ai divisé la première par la deuxième pour faire disparaître ds .....

**kdjender** · 18/04/2016, 22h26

Nom : Sans titre.png
Affichages : 270
Taille : 5,4 Ko

Bonsoir à tous, puisque il n'y a pas de solutions analytiques, pouvez vous me dire quelle méthode numérique que je peux utiliser pour résoudre ce système d’équations ?
Je précise que f et g ont le temps t comme variable (fonctions du temps).

invite52487760 · 18/04/2016, 23h37

Salut :

Ton Système est très joli car il contient beaucoup de symétries il me semble ( La symétrie la plus marquante ici est une rotation peut être ) ?

Ton système : $\text{[math]}$ avec : $\text{[math]}$ vérifie : $\text{[math]}$ .
Par conséquent : $\text{[math]}$
Regarde si ce système représente une particularité du système général : $\text{[math]}$ pour $\text{[math]}$ . On discutera de la suite après.
Aussi, peux tu nous dire pourquoi tu t’intéresses à ce système plus particulièrement ?
Cordialement.

invite52487760 · 18/04/2016, 23h47

excuse moi, j'ai fait une faute :
Je parle de : $\text{[math]}$ et non de $\text{[math]}$

**Resartus** · 18/04/2016, 23h53

Bonsoir,
Comme cela a été dit plus haut, on peut exprimer l'équation sous la forme suivante, avec z=f+ig :
z"+3z'/|z'|-(25-10i)z=0, soit z"=(25-10i)z-3z'/|z'|
La résolution numérique la plus simple est de partir d'un couple de départ z(0) et z'(0) (2 valeurs complexes, soit 4 valeurs réelles), de calculer z" à partir de l'équation, puis, en choisissant un pas dt assez petit, (par exemple 0,01), d'appliquer à chaque itération la formule z(t+dt)=z(t)+dt*z'(t) et z'(t+dt)=z'(t)+dt*z"(t).

Ce qu'on constate rapidement en faisant cette simulation, c'est que z diverge assez rapidement., et son argument finit par varier linéairement (ce qui revient à dire que f et g ont des oscillations quasi périodiques et de plus en grandes)
Cela peut se comprendre facilement : en effet, pour z assez grand, l'équation va se comporter comme z"=z(25-10i), dont, sauf réglage très précis des points de départ, la solution contiendra une exponentielle de la forme K0*exp(at)*exp(ibt) avec a=5,1.. et b=- 1,0... (a+ib=racine(25-10i)

Il est possible qu'il y ait des points de départ où les fonctions restent bornées.
Si ces solutions existent, je pense qu'elles doivent être instables, c'est à dire que la moindre variation du point de départ va conduire à la divergence

invite52487760 · 19/04/2016, 00h24

Je m'excuse, j'ai mal interpeter le résultat :
en fait, je voulais juste faire remarquer que peut etre : $\text{[math]}$ : $\text{[math]}$ . C'est tout. ( Invariance par rotation.

**Resartus** · 19/04/2016, 00h38

Oups Désolé, j'avais mal lu les équations.

En fait les équations s'écrivent z"=25z-10iz'-3z'/|z'|
Pour z assez grand, l'équation s'écrit z"=25z-10iz', dont les solutions sont de la forme (a+bt)exp(-(5it).
Les solutions ressemblent plus à des spirales d'archimède (croissance linéaire du module)

**kdjender** · 19/04/2016, 00h45

Excusez moi, mais la méthode de Runge Kutta ne serait t elle pas le meilleur des moyens pour les résoudre numériquement ?

**Resartus** · 19/04/2016, 09h33

Pourquoi pas.... Ce que j'ai écrit (méthode d'Euler) équivaut à l'ordre 1 de Runge-Kutta, et chaque ordre de plus améliorera la précision. Tout dépend de vos besoins de détail. Pour une équation en dérivée seconde, l'ordre 4 de Runge-Kutta est un bon début...

En y regardant de plus près, il semble intéressant de faire le changement de variable z=exp(-5it).y, ce qui ramène à une équation plus simple en y

Il est même possible que l'équation soit résoluble. Je vérifierai cela ce soir...

invite52487760 · 19/04/2016, 12h48

Salut :

Envoyé par chentouf

Salut :

Ton Système est très joli car il contient beaucoup de symétries il me semble ( La symétrie la plus marquante ici est une rotation peut être ) ?

Ton système : $\text{[math]}$ avec : $\text{[math]}$ vérifie : $\text{[math]}$ .
Par conséquent : $\text{[math]}$
Regarde si ce système représente une particularité du système général : $\text{[math]}$ pour $\text{[math]}$ . On discutera de la suite après.
Aussi, peux tu nous dire pourquoi tu t’intéresses à ce système plus particulièrement ?
Cordialement.

On peut montrer que : $\text{[math]}$ et $\text{[math]}$
Par conséquent :
$\text{[math]}$

Si on réussit à montrer que : $\text{[math]}$ est injective ou bijective, on aura alors : $\text{[math]}$
Par conséquent : L'ensemble des solutions de ton système est l'ensemble des solutions du système linéaire du premier ordre : $\text{[math]}$ avec : $\text{[math]}$ et $\text{[math]}$ .

Cordialement.

invite52487760 · 19/04/2016, 13h13

excusez moi, je corrige une erreur dans mon texte précédent :
Voici comment il devient :
==================
On peut montrer que : $\text{[math]}$ et $\text{[math]}$
Par conséquent :
$\text{[math]}$

Si on réussit à montrer que : $\text{[math]}$ est injective ou bijective, on aura alors : $\text{[math]}$
Par conséquent : L'ensemble des solutions de ton système est l'ensemble des solutions du système linéaire du premier ordre : $\text{[math]}$ avec : $\text{[math]}$ et $\text{[math]}$ .

Cordialement.

**kdjender** · 19/04/2016, 13h46

Bonjour Resartus, vous dites qu'avec Runge Kutta d'ordre 4 est un bon début, je dois comprendre qu'il y a un meilleur moyen pour la résoudre numériquement ? Bien évidement si nous trouvons une solutions analytique, je pense que je serais le plus heureux des hommes sur terre.

Pour ce qui est de l'écriture en nombre complexe, je l'ai déjà essayé, mais le module de Z m'a gêner, et je ne peux négliger le terme 3z'/|z'| sinon ca serait trop facile.

Bonjour chentouf, je ne vais pas vous mentir, mais je n'ai pas trop compris l'écriture matricielle, mais le peux que j'ai réussi à assimiler est que la forme de la solution peut être écrite comme vous l'avez indiquer.

Pour ce qui est des conditions initiales ce n'est pas un problème, nous pouvons proposer des valeurs non nulles. f(o) =/= 0 et g(o) =/= 0.

Ah au fait, je tiens à vous remercier tous comme vous êtes à m'aider sur ce problème mathématique, c'est vraiment très gentil de votre part.

invite52487760 · 19/04/2016, 13h55

Bonjour kdjender:

Envoyé par kdjender

Bien évidement si nous trouvons une solutions analytique, je pense que je serais le plus heureux des hommes sur terre.

Si ce n'est indiscret, est ce que c'est lié à un problème non encore résolu à l'heure actuelle ?

**kdjender** · 19/04/2016, 14h20

Envoyé par chentouf

Bonjour kdjender:

Si ce n'est indiscret, est ce que c'est lié à un problème non encore résolu à l'heure actuelle ?

Honnêtement je ne sais pas.

**Resartus** · 19/04/2016, 14h23

Je voulais juste dire qu'on peut toujours aller vers des ordres plus élevés, mais que cela demande des calculs plus longs...

Après le changement de variables, on arrive à une équation du type y"=-3(y'-5iy)/|y'-5iy|

Les fonctions y correspondantes varient plus lentement que les z (croissance approximativement polynomiale du second degré, puisque le module de la dérivée seconde est majoré par 3), et si vous devez faire une résolution numérique, cela donnera des résultats plus stables de la faire sur ces fonctions

En résumé, on aurait donc pour z un fond de rotation donné par le terme en e(-5it), multiplié par un facteur y
Cela veut dire que les fonctions initiales f et g se comportent à peu près comme des cos(5t+phi) et sin(5t+Phi) multipliés par un terme croissant lentement.

Pour ce qui est de la résolution analytique, à vu de nez, on devrait pouvoir trouver pour y/y' certaines solutions polynomiales exactes(a vérifier si vous avez le temps), mais je ne suis pas sûr que toutes puissent être obtenues comme cela

**kdjender** · 23/04/2016, 15h11

Envoyé par Resartus

Je voulais juste dire qu'on peut toujours aller vers des ordres plus élevés, mais que cela demande des calculs plus longs...

Après le changement de variables, on arrive à une équation du type y"=-3(y'-5iy)/|y'-5iy|

Les fonctions y correspondantes varient plus lentement que les z (croissance approximativement polynomiale du second degré, puisque le module de la dérivée seconde est majoré par 3), et si vous devez faire une résolution numérique, cela donnera des résultats plus stables de la faire sur ces fonctions

En résumé, on aurait donc pour z un fond de rotation donné par le terme en e(-5it), multiplié par un facteur y
Cela veut dire que les fonctions initiales f et g se comportent à peu près comme des cos(5t+phi) et sin(5t+Phi) multipliés par un terme croissant lentement.

Pour ce qui est de la résolution analytique, à vu de nez, on devrait pouvoir trouver pour y/y' certaines solutions polynomiales exactes(a vérifier si vous avez le temps), mais je ne suis pas sûr que toutes puissent être obtenues comme cela

Bonjour Resartus, jugez vous que la résolution analytique de ce système est toujours envisageable ?
Sinon pour ce qui est de Runge Kutta d'ordre 4, je crois que je n'arrive pas à le faire lorsque on a deux fonctions différentes (f et g), en gros je ne sais pas le faire pour un système d’équations différentielles, pouvez vous m'aider la dessus si c'est possible ? Et merci.

Equations différentielles couplées