Courbe paramètrée

[Hairah]

Bonsoir,

Ce dernier chapitre a été survolé par mon prof de TD, du coup j'aimerai bien avoir votre aide pour cette exercice et surement d'autres pour m’entraîner.

Voici l’énoncé :
Soit B(t) la courbe paramétrée définie par x(t) = t^2 + 2/t et y(t) = t^2 + 1/t^2

1) Trouver le point stationnaire et dessiner l'allure de la courbe en ce point.

2) Montrer que cette courbe a un point double. Donner ses coordonnées.

3) Montrer que la courbe a une asymptote quand t tend vers l'infini. Trouver l'équation de cette asymptote et la position de la courbe par rapport à celle-ci.

4) Etudier le sens de variation des fonctions coordonnées. Déterminer le point où la tangente est horizontale. Dessiner la courbe.


Du coup, pour la 1) on calcule la dérivée des deux fonctions et je trouve que le point stationnaire est quand t = 1 soit, (x(1), y(1)) = (3, 2)

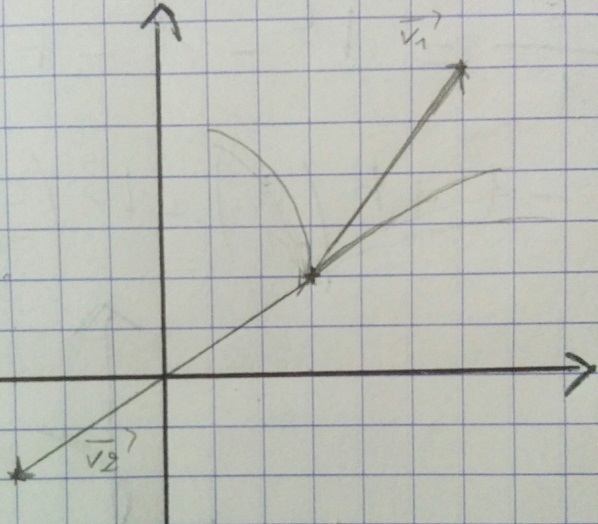
Pour l'allure ça coince, on nous a donné un exemple sur des courbes paramétrées avec un point singulier en 0 avec deux vecteurs non colinéaire grâce à des développements limités.
De ce que j'ai compris, si le coef devant le deuxième vecteur est positif en t+(puis t-) alors la courbe est attiré par le vecteur 2 sinon si c'est négatif alors elle est repoussée. Donc ici on a un point de rebroussement de 2 espèces puisque c'est forcément positif. Non ?

Mais pour le coef du premier vecteur, il sert à quoi ? Pour savoir c'est dans le sens direct ou indirect ?
-----

[God's Breath]

Bonjour,

Je ne comprends pas ta méthode d'étude du point stationnaire avec le signe des coefficients du développement limité.
Ce sont les degrés des termes qui interviennent dans le développement limité qui permettent de conclure.

Que trouves-tu comme développement limité ?

[Hairah]

Difficile d'expliquer quand on a pas vraiment compris

Pour les développements limités je trouve :
x(t) = 3 + 3 (t-1)² - 6 (t-1)³ + o((t-1)^4)

y(t) = 2 + 4 (t-1)² - 4 (t-1)³ + o((t-1)^4)

[God's Breath]

En notant , et , les vecteurs et sont linéairement indépendants et :



donc, dans le repère , la courbe a l'allure de ...

[A voir en vidéo sur Futura]

[Hairah]

Je suppose que h tend vers 0.

Donc il y a un point de rebroussement de 1 espèce puisque h² est pair et h³ est impaire.

Et on a une allure de courbe dans ce style ?

[God's Breath]

Oui, h tend vers 0 puisqu'on développe au voisinage de t=1 qui donne le point stationnaire.

On obtient effectivement un point de rebroussement de première espèce.

[Hairah]

D'accord merci !

Pour la suite

la 2) je trouve et tel que

Pour la 3), je trouve comme asymptote et au dessus de la courbe.
On doit bien étudier y'(t) - t pour la position de l'asymptote ?

Pour la 4), le point où la tangente est horizontale c'est quand et uniquement lui (j'entends par là que x'(t) doit être différent de 0) ?

Si c'est bien le cas le point est

[God's Breath]

Pour la question 2, c'est bon.

On doit bien étudier y'(t) - t pour la position de l'asymptote ?[/TEX]

Non, si l'asymptote est d'équation y=ax+b, tu dois étudier le signe de y(t)-ax(t)-b, donc ici de y(t)-x(t) pour conclure que :
— si y(t)>x(t) la courbe est au-dessus» de l'asymptote ;
— si y(t)>x(t) la courbe est au-dessous» de l'asymptote

our la 4), le point où la tangente est horizontale c'est quand et uniquement lui (j'entends par là que x'(t) doit être différent de 0) ?

Oui, c'est bien ça. Je n'ai pas vérifié les coordonnées que tu obtiens.

[Hairah]

D'accord merci !