Physicien en mathématiques

[Quantique94]

Salut tout le monde , je suis étudiant en master de physique théorique j'ai des problèmes en mathématiques je n'arrive pas a résoudre des problèmes de lycée que faire pour se remettre au niveau merci
-----

[invite8cc8b94d]

Bonsoir,

Il est étonnant que vous soyez arrivé jusqu'en master sans savoir résoudre des problèmes de lycée !

Qu'est-ce que vous appelez "problèmes de lycée" exactement, une équation du second degré, dériver une fonction?

Peut être c'est exagéré, mais n'oubliez pas que la physique à ce niveau, c'est essentiellement des équadiff aux dérivées partielles, algèbre, Hilbert, du Fourier etc, ce qui demande quand même d'avoir certaines bases dans ces différents domaines des mathématiques.

Vous avez vu ces différents concepts lors de vos modules de maths durant la licence j'imagine ?

Lazar

[Quantique94]

Non , pas ce genre de choses les EDP, intégrales, dérivées même l'equation de Schrödinger dans certaines situations ça va ,aussi mais quand il s'agit de problèmes de lycée ou il faut réfléchir je bloque un peu

[Quantique94]

En licence j'ai vus pas mal de choses j'ai fais 8 modules de mathématiques durant ma licence

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Ton questionnement semble dire : "Appliquer des formules toutes faites, même compliquées, je sais faire. Mais quand il faut décider quelle formule sera à appliquer, même sur des cas simples, je n'ai pas l'habitude". (*)
Si c'est ça, c'est seulement une question d'habitude (qu'il aurait fallu prendre avant le lycée, mais il n'est pas trop tard). Qui va te demander un bel effort, si tu veux changer ça. Tu peux par exemple copier sur Internet ou scanner dans des livres un certain nombre d'exercices de collège et lycée, en éliminant les références au chapitre correspondant. Puis, après les avoir mélangés, tu les fait. Tu vas t'apercevoir, à ta grande surprise, que tu as oublié (ou jamais apprises) un certain nombre de propriétés élémentaires. Du coup, tu les apprendras, ce qui te fera un background. Et tu progresseras vite.
Il est possible que je me trompe d'interprétation. Ne te vexe pas, j'ai lu ce que je pouvais. Et réexplique qu'on approfondisse.

Cordialement.

(*) Ça arrive fréquemment aux néo-profs.

[mmanu_F]

Salut,

tu pourrais donner un exemple concret d'exercice de lycée que tu n'arrive as à faire ? ça aiderait à localiser ton problème.

[Quantique94]

Bonsoir et merci pour les réponses , je vais donner un exemple

[mmanu_F]

Bonsoir et merci pour les réponses , je vais donner un exemple
Pièce jointe 326930

ok. maintenant explique-moi ta démarche en fasse de ce problème.

[gg0]

Ok, Quantique 94.

Ce n'est pas un exercice élémentaire pour lycéen, mais on peut faire quelque chose avec. Et effectivement, en n'utilisant que des règles de niveau lycée. mais dans un contexte inhabituel si on n'a pas fait ce genre d'exercice.

Face à un système d'équations, à quoi penses-tu ?

Cordialement.

Nb : On n'est pas dans le cas que j'avais développé au message #5.

[Quantique94]

Face a un système d’équations je pense aux méthodes matricielles ,en physique c'est souvent plusieurs équations

[Quantique94]

---

Le démarche je pense qu'il faut écrire une équation du second dégrée et imposé un signe positif ou nul au discriminant mais j'ai mis trop de temps pour résoudre :/

[gg0]

Penser en termes de matrices est un automathisme (*), qui t'empêche de regarder vraiment ta question. Ici, ce n'est pas un système linéaire.

"La démarche je pense qu'il faut écrire une équation du second degré" ???? Non il faut traiter la question. Que sais-tu faire sur les systèmes d'équation, en dehors de ce que tu as fait en licence sur des systèmes particuliers. En quatrième et troisième, tu n'avais pas les matrices.

Finalement, tu as effectivement besoin de revoir les méthodes du lycée, de savoir faire les calculs faciles.

Cordialement.

(*) Oui, avec un h comme maths. Une réaction non pensée, une action qui n'est pas la stricte application d'une règle (souvent, la règle n'est pas vraiment connue, mais le calcul imité).

[Quantique94]

Oui si c'est pas un système linéaire on utilisait la substitution , ou a la fac du numérique a condition de vérifier la convergence de la solution

[gg0]

Eh bien ici, que donne la substitution ?

[Quantique94]

je trouve

[mmanu_F]

je trouve Pièce jointe 326947

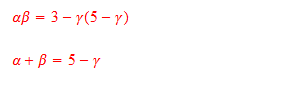
ok, c'est un premier mouvement intéressant, qu'est ce que tu tentes (as tenté) ensuite ? c'est un jeu de manipulation, il faut manipuler

[gg0]

C'est une façon de faire, j'aurais plutôt essayé d'éliminer une variable dans une équation (*), par exemple gamma qui se calcule dans la deuxième en fonction des deux autres peut être remplacé dans la première.
mais on peut y arriver avec ton calcul, de façon plus compliquée.

Cordialement.

(*) C'est le plus souvent ce qu'on fait dans la méthode de substitution.

NB : En appelant a, b et c les variables, tu pourras écrire directement dans le message. Les pièces jointes, ça peut prendre du temps (validation par le forum)

[Quantique94]

mais si je supprime gamma comment obtenir une condition ?

[gg0]

Ben ... ça vient tout seul.

Au lieu de demander "si ..." regarde ce que ça donne.

[CARAC8B10]

Bonjour,
En utilisant x, y, z :
xy + yz+xz=3
x+y+z=5

Tu peux remarquer que le système est inchangé si tu permutes x et y ou y et z ou x et z
Donc tu peux éliminer n'importe laquelle de ces inconnues pour obtenir une relation de degré 2 en ces 2 autres inconnues que tu peux résoudre au choix comme une équation du second degré en l'une ou l'autre de ces inconnues.

Par exemple en éliminant x :
on peut au choix résoudre l'une de ces 2 équations en y ou en z :
ou


La condition d'existence de racines réelles de ces 2 équations te fournit l'une ou l'autre de ces 2 inéquations :
ou

Au final on obtient les conditions

[bdom001]

Bonjour,

La condition d'existence de racines réelles de ces 2 équations te fournit l'une ou l'autre de ces 2 inéquations :
ou

Au final on obtient les conditions

Vos inéquations sont justes mais leur résolution est fausse.

[mmanu_F]

Salut,

je suis étudiant en master de physique théorique j'ai des problèmes en mathématiques

il me semble, après ces quelques échanges de messages, que ça ne t'amuse pas beaucoup de chercher à craquer ce genre de petites énigmes mathématiques...

alors du coup je me demande pourquoi tu as choisi un master de physique théorique, étant donné que le boulot principal d'un physicien théoricien est (en caricaturant un peu) de traduire la Nature en termes mathématiques et de craquer les énigmes mathématiques qui apparaissent dans le processus. Pourquoi ne pas avoir choisi une filière plus tournée vers l'expérimentation ?

[ansset]

Bonjour,
Vos inéquations sont justes mais leur résolution est fausse.

certes, ceci dit je n'ai pas encore vu la démo complète qui aboutie à l'intervalle de l'énoncé.
je crois qu'on y arrive en réinjectant les premiers intervalles trouvés dans les équations.
Cdt

[ansset]

perso, je trouve [-1;3] , pas de 13/3 !

[CARAC8B10]

Mais pourquoi ai-je pris 16 pour racines carrée de 64 ? (déjà un effet Trump) ?
Donc, bien sûr : soit et

Question bonus :
Pourrait-on avoir une "visualisation" géométrique : intersection du plan d'équation x+y+z-5=0 et de la surface d'équation xy+yz+xz-3 = 0 ?
Mais comment caractériser cette dernière surface ?

[ansset]

edit inutile.

[CARAC8B10]

certes, ceci dit je n'ai pas encore vu la démo complète qui aboutie à l'intervalle de l'énoncé.
je crois qu'on y arrive en réinjectant les premiers intervalles trouvés dans les équations.
Cdt

Rine que de plus classique :
Si on choisit d'éliminer x
qui substitué dans l'autre équation donne :

soit , au choix, à résoudre :

ou

La résolution de (1) dans R exige que son discriminant soit soit :

soit y "entre" les racines : et

[bdom001]

certes, ceci dit je n'ai pas encore vu la démo complète qui aboutie à l'intervalle de l'énoncé.
je crois qu'on y arrive en réinjectant les premiers intervalles trouvés dans les équations.
Cdt

Bonjour,
personnellement, je me contente d'étudier la variation de la fonction :

cette fonction est strictement croissante pour
puis strictement décroissante pour

La fonction f s'annulant pour les 2 racines centrées sur la valeur 5/3, cette fonction f est positive ou nulle pour

Ceci dit, cela n'explique pas à notre ami Quantique94 comment faire pour atteindre le niveau de la terminale scientifique ...

[ansset]

oui, oui, pas de soucis.
j'ai juste fait une première erreur de calcul, qui m'a entraîné vers un truc inutile et plus complexe.

[ansset]

Ceci dit, cela n'explique pas à notre ami Quantique94 comment faire pour atteindre le niveau de la terminale scientifique ...

re-
je ne parlerai pas ici de "niveau" mais d'habitude de calcul et d'un peu d'astuce.
je pense même que ce petit exo ( qui ne fait appel qu'aux notions de lycée ) pose des soucis à beaucoup d'élèves de TS. (*)
la seule idée qui me vient est de suggérer de refaire des exos...

(*) même à des vieux comme moi qui ont dépassé le niveau bac, et peuvent faire des trucs bien plus compliqués et qui pourtant ne sont pas à l'abri d'un calcul trop rapide ( car la direction de solution vient assez vite ) et d'une boulette.