Bonjour,
Je ne savais pas poster ma question ici ou dans la catégorie lycée mais je suis dans le supérieur alors on va considéré que c'est du sup..
J'essaye, sans y arriver, de trouver la limite en -inf de
Avez-vous une piste ? (Hospital autorisé mais je pense pas qu'il y en a besoin ici)
Merci d'avance !
-----




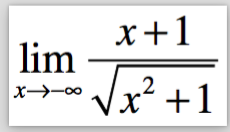
 , ce qui revient au même : on n'est donc pas plus avancé, et Hospital ne semble pas être approprié...
, ce qui revient au même : on n'est donc pas plus avancé, et Hospital ne semble pas être approprié...