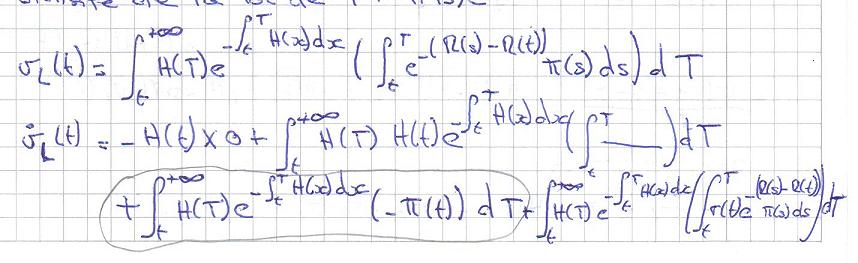Bonjour,
Je dois calculer une dérivée d'une fonction qui comprend une intégrale, la variable de dérivation est la borne inférieure de l'intégrale et est également contenue dans l'expression sous le signe somme.
J'ai le résultat mais je suis pas sûr de comprendre et d'être capable de le refaire...
J'ai joint le scan de la fonction et du calcul de la dérivée.
PS : suis pas sûr d'être dans le bon forum mais je me souviens pas avoir ces trucs pour le bac
Salut !
Tu peux peut-être utiliser les propriétés de l'exponentielle pour faire sortir de l'intégrale ce qui dépend de t.
Bonjour.
N'est-ce pas d(r(t))/dt en facteur de v(t) plutôt que r(t) ?
Pour dériver celà, tu peux déjà sortir le "exp(r(t))" de ton intégrale, puis ensuite utiliser la formule qui te permet de dériver u*v. (où u vaut r(t) et v vaut ton intégrale).
Je ne suis pas un habitué de la dérivée d'une intégrale. Surtout dans ce cas ou la variable de dérivation n'est pas la variable muette du somme.
Dans mon idée, il faut d'abord dériver pour le t en tant que borne puis dériver la fonction sous le somme.
J'approche?
Non pas du toutEnvoyé par somnambulie
Il y a des théorèmes qui te permettent de dériver à l'intérieur d'une intégrale mais ces théorèmes fonctions quand les bornes sont fixes. On peut s'y ramener en faisant des changements de variable.
Mais ici, la situation est plus simple : tu peux faire sortir la quantitéde ton intégrale ; tu te retrouves alors avec quelque chose de la forme
C'est un produit de fonctions que tu dois savoir dériver : pour la première c'est simple et pour la seconde, la dérivée est juste
J'ai trouvé un résultat cohérent avec la méthode que vous proposez.
J'ai un autre prb du même type que je n'arrive pas à traiter avec la même méthode, cf. nlle image jointe.
Cette je ne crois pas pouvoir simplifier l'expression avant de dériver, mais je dois me tromper.
Merci pour votre aide
