Salut,
Comment déterminer le cardinal de l'ensemble des matrices de la forme suivante ? J'ai démontrer qu'elles appartenaient à On(R) les matrices orthogonales en faisant le produit de matrice par bloc ... Je dois en déduire le cardinal de On(R)
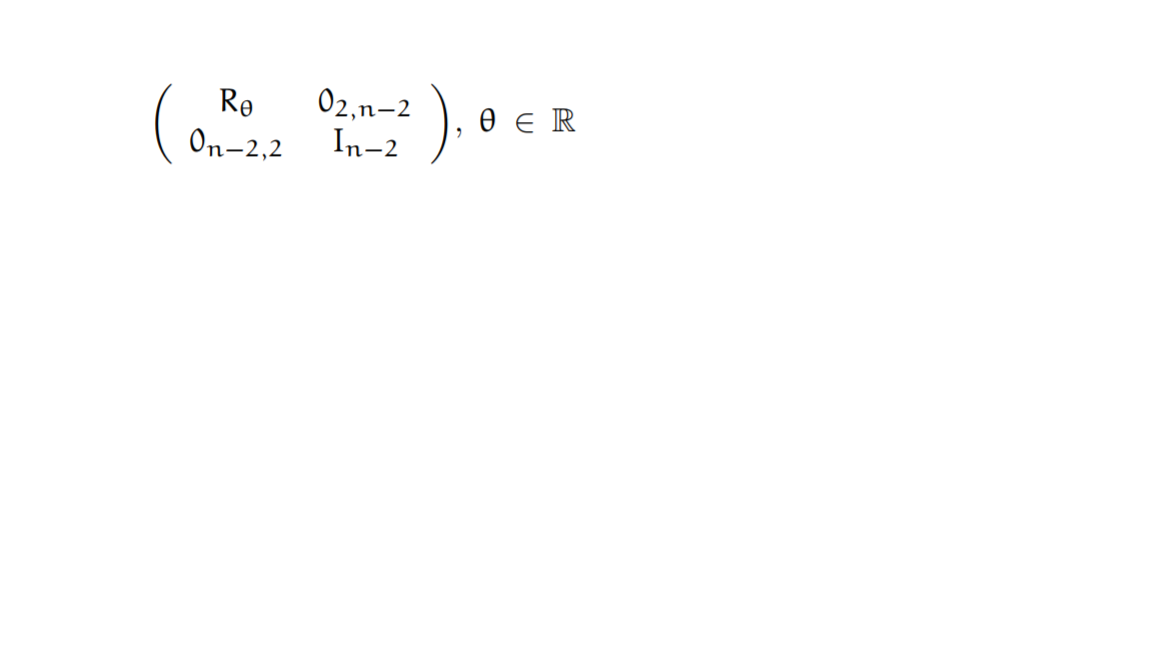
-----



 et
et 